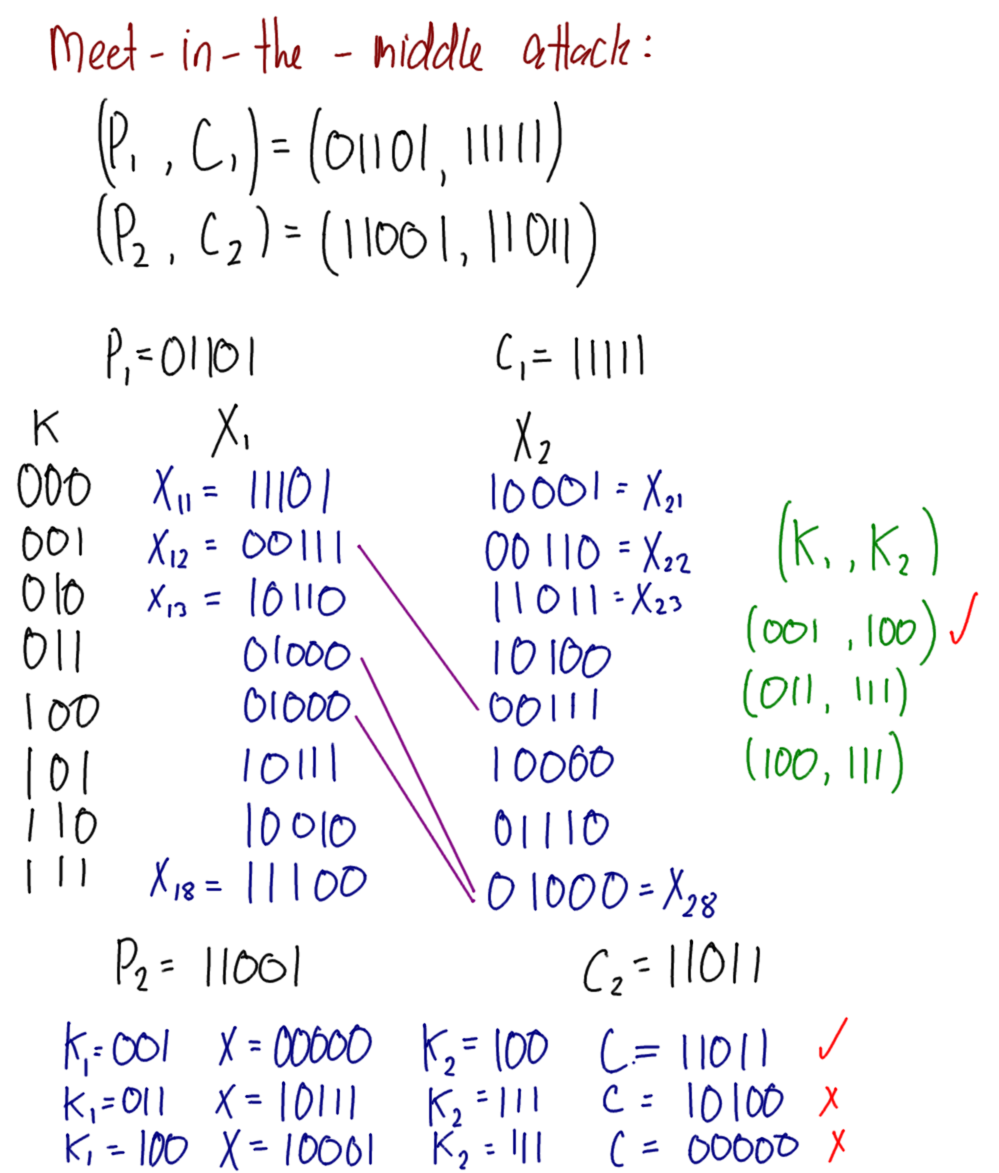Chapter 7
Encryption and Attacks
7.2 Attacks on Encryption
7.2.1 Aims and Knowledge of the Attacker
7.2.2 Brute Force Attacks
7.2.3 Cryptanalysis
7.2.4 Measuring Security
7.3 Block Cipher Design Principles
7.4 Stream Cipher Design Principles
7.5 Example: Brute Force on DES
7.6 Example: Brute Force on AES
7.7 Example: Meet-in-the-Middle Attack
7.8 Example: Cryptanalysis on Triple-DES and AES
File: crypto/encryption.tex, r1965
Chapter 6 introduced concepts of encryption using classical ciphers. This chapter formalises these concepts, in Section 7.1 defining the building blocks for encryption in modern ciphers, in particular in symmetric key cryptography. Section 7.2 looks at encryption from the attackers point of view. Understanding the approaches attackers can take is necessary to be able to build secure systems with will withstand attacks. Section 7.3 and Section 7.4 outline the general design approaches to the two types of symmetric key ciphers: block ciphers and stream ciphers.
Further details about encryption and attacks are covered in subsequent chapters, including details on Data Encryption Standard (DES) (Chapter 8) and Advanced Encryption Standard (AES) (Chapter 9). The alternative to symmetric key encryption, public key cryptography is introduced in Part IV.
Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).
7.1 Encryption Building Blocks
Video: Encryption Building Blocks (13 min; Mar 2020)
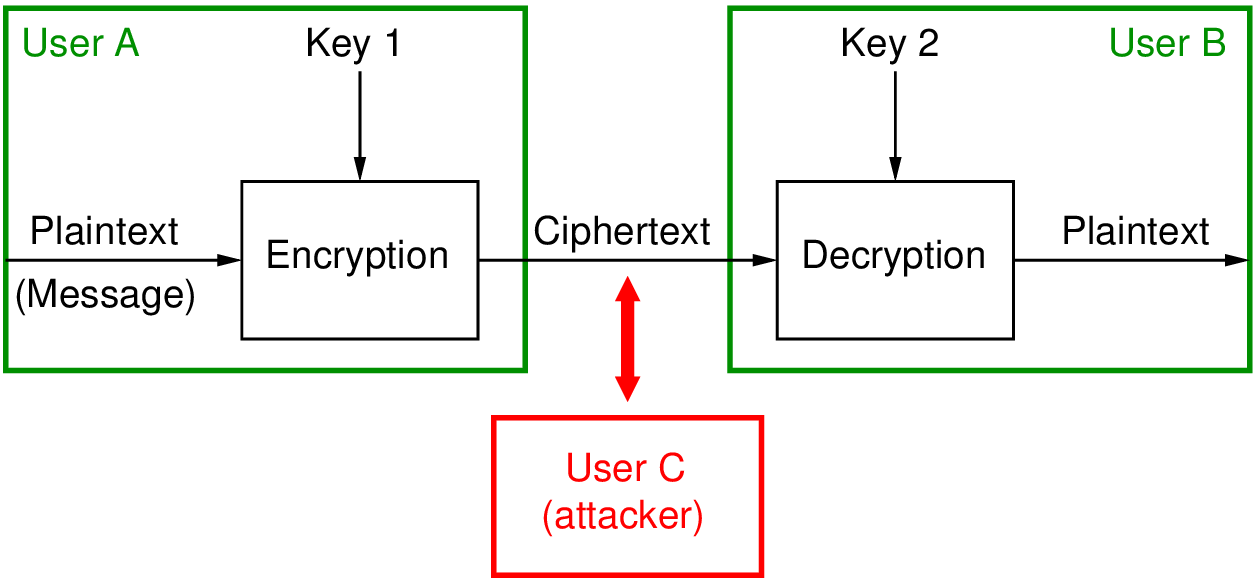
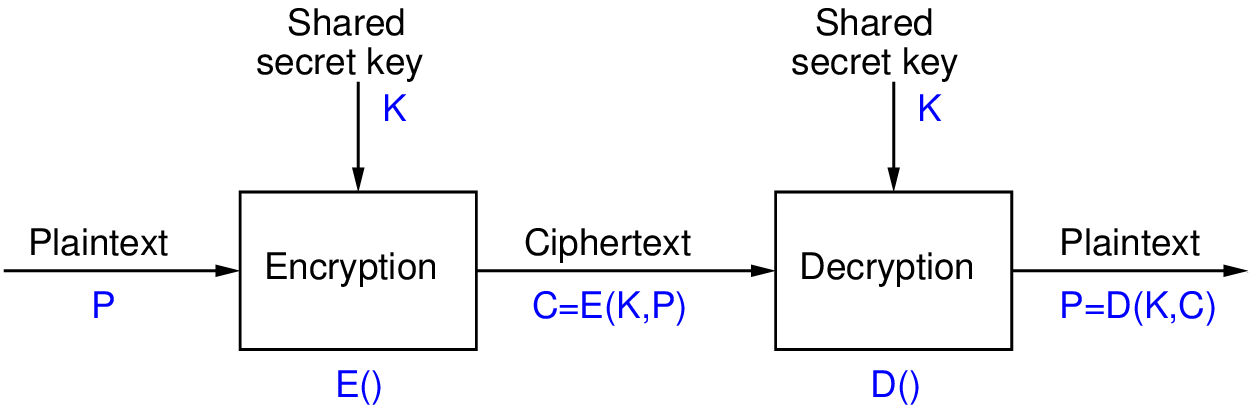
Figure 7.1 shows the general model for encrypting for confidentiality that we have seen previously.
- Symmetric
- sender/receiver use same key (single-key, secret-key, shared-key, conventional)
- Public-key
- sender/receiver use different keys (asymmetric)
All ciphers until about the 1960’s were symmetric key ciphers. The encrypter and decrypter used the same key, i.e. symmetry between the keys. The key must be shared between the two users and kept secret.
A new form of cryptography was designed in the 1960’s and 1970’s, where the encrypter uses one key and the decrypter uses a different but related key. The keys are asymmetric. One of the keys is kept secret, while the other can be disclosed, i.e. made public.
We will focus on symmetric key ciphers initially, and return to public-key ciphers later.
We often use simple mathematical notation to describe the steps. E() is a function that takes two inputs: key K and plaintext P. It returns ciphertext C as output. E() represents the encryption algorithm. D() is the decryption algorithm.
Symmetric key encryption is the oldest form of encryption and involves both parties (e.g. sender and receiver) knowing the same secret key. Plaintext is encrypted with the secret key, and the ciphertext is decrypted with that secret key. If anyone else (i.e attacker) learns the secret key, then the system in not secure.
For symmetric key encryption to be secure, the algorithm must be well designed (strong, not easy to break) and the secret key must be kept secret. AES is an example of a strong algorithm, and it uses keys of length 128 bits or longer. One of the challenges of symmetric key encryption is informing the receiver of the secret key in advance: it must be done in a secure manner.
- Substitution
- replace one element in plaintext with another
- Permutation
- re-arrange elements (also called transposition)
- Product systems
- multiple stages of substitutions and permutations, e.g. Feistel network, Substitution Permutation Network (SPN)
Symmetric key ciphers are designed around two basic operations: substitution and permutation. We have seen these operations when looking at classical ciphers. We also saw the principle that repeating the operations can make a cipher more secure. Modern ciphers are designed using these two basic operations, but repeated multiple times. For example, perform a substitution and then permutation, then repeat. The result is a “product system”.
The Feistel network and SPN are two common design principles for modern ciphers and will be mentioned later when discussing block ciphers like AES and DES.
- Block cipher
- process one block of elements at a time, typically 64 or 128 bits
- Stream cipher
- process input elements continuously, e.g. 1 byte at a time, by XOR plaintext with keystream
Originally the idea was that block ciphers were suitable for processing large amounts of data when there were no strict time constraints. Stream ciphers were fast and suitable for real-time applications. For example, for encrypting real-time voice, as the data (plaintext) is generated, it needs to be quickly encrypted and then the ciphertext transmitted across a network. By encrypting only a small amount of plaintext at a time and using the extremely fast XOR operation, stream ciphers could perform the encryption without introducing significant delay.
However nowadays, the dedicated hardware support for block ciphers like AES, there is not a significant difference in performance (delay) of block and stream ciphers. Hence we see block ciphers (in particular, AES) used in scenarios for which stream ciphers were originally designed for.
We will focus on block ciphers initially, and return to stream ciphers later.
- Data Encryption Standard (DES)
- Became a US government standard in 1977 and widely used for more than 20 years; key is too short
- Advanced Encryption Standard (AES)
- Standardised a replacement of DES in 1998, and now widely used. Highly recommended for use.
While no longer recommended or in widespread use, DES was the first cipher that saw widespread use. The primary limitation of DES however was the key was eventually subject to a brute force attack. It was only 56 bits.
While Triple DES, which used the original DES but expanded the key length, was popular for awhile, a new cipher was needed to perform well in a variety of hardware platforms. AES was standardised in 1998 and continues to be the recommended symmetric key block cipher for most applications today. There are no known practical attacks that cannot be defended.
DES and AES are covered in depth later.
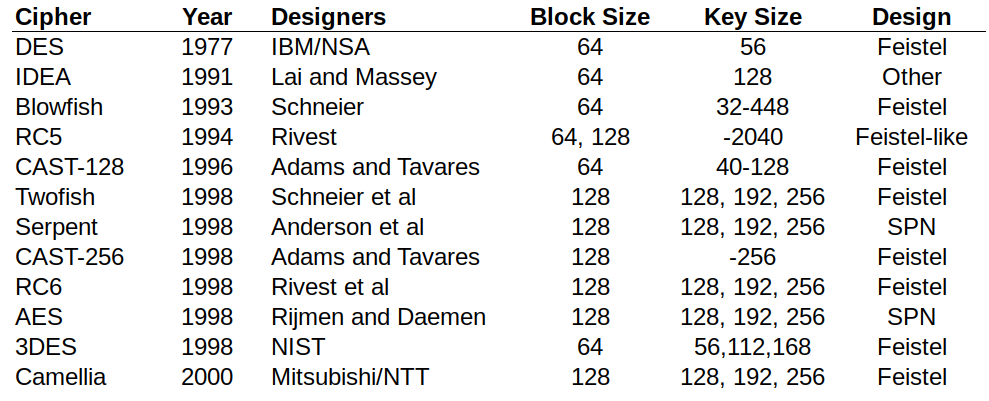
Figure 7.3 lists common symmetric key encryption block ciphers starting with DES, through to around the time of AES. Most block ciphers operate on blocks of 64 or 128 bits, and support a range of key lengths. There are three main design principles: Feistel network or structure, Substitution Permutation Network, or Lai-Massey.
AES is still highly recommended for most applications. There have been newer proposals since then, however very few are standards or see wide spread usage. A recent trend is on developing “lightweight” ciphers that perform well on very small devices, e.g. sensors.
A detailed review of block ciphers is Roberto Avanzi’s “A Salad of Block Ciphers: The State of the Art in Block Ciphers and their Analysis”, 2017, which is available for free at https://eprint.iacr.org/2016/1171.pdf
7.2 Attacks on Encryption
Cryptography, which is the study of cipher design, and cryptanalysis, i.e. breaking cipher designs, go hand-in-hand. Together these areas are study are cryptology. Let’s now look from the attackers perspectives. Note that when we use the word “attacker”, we don’t necessarily mean a malicious entity. That is, we are not judging whether the entity performing the attack is good or evil.
Video: Attacks on Encryption (28 min; Mar 2020)
7.2.1 Aims and Knowledge of the Attacker
First we list the general aims of an attacker, as well as assumptions we often make about the attacker.
- Study of ciphers and attacks on them is based on assumptions and requirements
- Assumptions about what attacker knows and can do, e.g. intercept messages, modify messages
- Requirements of the system/users, e.g. confidentiality, authentication
- Normally assumed attacker knows cipher
- Keeping internals of algorithms secret is hard
- Keeping which algorithm used secret is hard
- Attacker also knows the ciphertext
- Attacker has two general approaches
- “Dumb”: try all possible keys, i.e. brute force
- “Smart”: use knowledge of algorithm and ciphertext/plaintext to discover unknown information, i.e. cryptanalysis
7.2.2 Brute Force Attacks
Brute force is the “dumb” or naive approach an attacker can take. It involves trying keys until the correct plaintext is found.
| Key | Key | Worst case time at speed:
| ||
| length | space | /sec | /sec | /sec |
| 32 | 4 sec | 4 ms | 4 us | |
| 56 | 833 days | 20 hrs | 72 sec | |
| 64 | 584 yrs | 213 days | 5 hrs | |
| 80 | yrs | yrs | 38 yrs | |
| 100 | yrs | yrs | yrs | |
| 128 | yrs | yrs | yrs | |
| 192 | yrs | yrs | yrs | |
| 256 | yrs | yrs | yrs | |
| 26! | yrs | yrs | yrs | |
Table 7.1 shows, for different key lengths, the time it takes to try every key if a single computer could make attempts at one of three rates: per second, per second, or per second. There are not necessarily realistic speeds, although roughly represent lower and upper limits for today’s computing power.
While this table presents the worst case time, in most cases, it is not much different from the average time. Recall the average time is about half of the worst case time. For a 128 bit key at decrypts per second, the worst case time is about years, and the average time is about . That is, both about years. With such large times, cutting the time in half makes no practical difference.
Note that the last line is for a key for a monoalphabetic English cipher. There are 26! possible keys which is equivalent to a binary key of about 88 bits.
For comparison, the age of the Earth is approximately years and the age of the universe is approximately years.
7.2.3 Cryptanalysis
Cryptanalysis is the “smart” approach to breaking ciphers. The attacker uses knowledge of the ciphers, as well as expected patterns in ciphertext and plaintext to find unknown information (e.g. keys or plaintext).
Attacks on ciphers can be classified based on how much information an attacker is assumed to know to successfully perform the attack. We describe different classifications in the following.
- Ciphertext Only Attack
- Known Plaintext Attack
- Chosen Plaintext Attack
- Chosen Ciphertext Attack
- Chosen Text Attack
We describe the different attacks in the following.
Ciphertext Only Attack
- Attacker knows:
- encryption algorithm
- ciphertext
- Hardest type of attack
- If cipher can be defeated by this, then cipher is weakest
The common assumption is that an attacker knows the encryption algorithm and ciphertext, and that they had no influence over the choice of ciphertext. This is referred to a ciphertext only attack. A cipher that is subject to a ciphertext only attack is the weakest of the groups of attacks we will consider.
However if a cipher cannot be defeated by a ciphertext only attack, then it still may be defeated if the attacker has additional information. The following defines these additional attacks. They all assume the attacker has the same information as a ciphertext only attack (i.e. encryption algorithm and ciphertext), but also make additional assumptions about other known information and the ability to select/influence values. Generally, the more information an attacker knows or can control, the easier their task of defeating a cipher.
Known Plaintext Attack
- Attacker knows:
- encryption algorithm
- ciphertext
- one or more plaintext–ciphertext pairs formed with the secret key
- E.g. attacker has intercept past ciphertext and somehow discovered their corresponding plaintext
- All pairs encrypted with the same secret key (which is unknown to attacker)
In a Known Plaintext Attack (KPA), the attacker also has access to one or more pairs of plaintext/ciphertext. That is, assume the ciphertext known, , was obtained using key and plaintext (either of which the attacker is trying to find). The attacker also knows at least and , where is the output of encrypting with key . That is, the attacker knows a pair . They may also know other pairs (obtained using the same key ).
How could an attacker known past plaintext/ciphertext pairs? A simple example is if the plaintext messages were only valid for a limited time, after which they become public. Such as coordinates for a public event to take place. Before the event takes place the coordinates are encrypted and secret. But after the event takes place, while the coordinates were decrypted, the attacker has learnt the value of the coordinates/plaintext (without knowing the key).
Generally, the more pairs of plaintext/ciphertext known, the easiest it is to defeat a cipher.
Chosen Plaintext Attack
- Attacker knows:
- encryption algorithm
- ciphertext
- plaintext message chosen by attacker, together with its corresponding ciphertext generated with the secret key
In a Chosen Plaintext Attack (CPA) the attacker is able to select plaintexts to be encrypted and obtain their ciphertext (but not knowing the key used in the encryption). In such an attack, the attacker may select plaintext messages that have characteristics that make it easier to break the cipher. Ability to select plaintext and have it encrypted is common for public key ciphers (since the encryption key is public but the decryption key is private), which should be designed to be resistant to such attacks.
Chosen Ciphertext Attack
- Attacker knows:
- encryption algorithm
- ciphertext
- ciphertext chosen by attacker, together with its corresponding decrypted plaintext generated with the secret key
- Attackers aim is to find the secret key (not the plaintext)
In a Chosen Ciphertext Attack (CCA) the attacker chooses a ciphertext, and obtains the corresponding plaintext, in an attempt to discover a secret key. Note in this attack, the aim is to find the secret key. If the attacker has a way to obtain plaintext from a chosen ciphertext, then they could simply intercept ciphertext to find plaintext. A CCA normally involves the attacker tricking a user to decrypt ciphertext and provide the plaintext.
There are variations of the above types of attacks, and the details of the attacks may be quite different, however this classification is sufficient to demonstrate that successful cryptanalysis depends partially on the amount of information known to the attacker.
7.2.4 Measuring Security
Is a cipher security? To answer such a question, methods of measuring security must be defined.
- Unconditionally Secure
- Ciphertext does not contained enough information to derive plaintext or key
- One-time pad is only unconditionally secure cipher (but not very practical)
- Computationally Secure
- If:
- cost of breaking cipher exceeds value of encrypted information
- or time required to break cipher exceeds useful lifetime of encrypted information
- Hard to estimate value/lifetime of some information
- Hard to estimate how much effort needed to break cipher
In theory we would like an unconditionally secure cipher. However in practice, we aim for computationally secure. Unfortunately it is difficult to measure if a cipher is computationally secure. For modern ciphers their security is judged based on the known theoretical and practical attacks (e.g. resistant to CCA or not) as well as the metrics in the following.
- Time:
- usually measured as number of operations, since real time depends on implementation and computer specifics
- Operations are encrypts or decrypts; ignore other processing tasks
- E.g. worst case brute force of -bit key takes (decrypt) operations
- Amount of Memory:
- temporary data needed to be stored during attack
- Known information:
- number of known plaintext/ciphertext values attacker needs to know in advance to perform attack
While time to break the cipher is the metric of interest, it is usually simplified to number of operations. For cryptanalysis, successful attacks should take fewer operations than brute force. That is, an attack that takes more operations the a brute force attack is considered an unsuccessful attack.
Often attacks requires intermediate values to be stored in memory while performing the attack. The less memory needed, the better the attack.
As seen in the previous classification, known plaintext, chosen plaintext and chosen ciphertext attacks all require the attacker to know additional information. The more information necessary for the attack to be successful, the poorer the attack is. For example, a known plaintext attack that will be successful if 1,000,000 pairs of plaintext/ciphertext are known, is better than a known plaintext attack that requires 2,000,000 pairs.
Video: Measuring Attacks on Ciphers (4 min; Mar 2021)
7.3 Block Cipher Design Principles
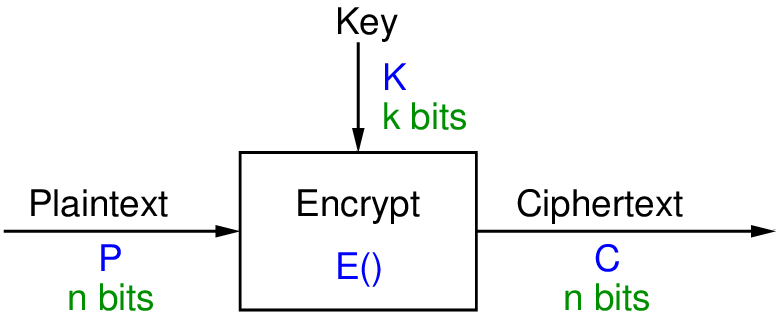
Block ciphers are the most common type of ciphers. They are designed to encrypt a single fixed length block of bits.
- Encrypt a block of plaintext as a whole to produce same sized ciphertext
- Typical block sizes are 64 or 128 bits
- Modes of operation used to apply block ciphers to larger plaintexts
Modes of operation are covered in Chapter 11.
Video: Block Cipher Design Principles (9 min; Mar 2021)
Let’s look at some simple, ideal block ciphers to illustrate basic concepts, which will then lead to common design principles used to create block ciphers in use today. In its simplest form, a block cipher maps an -bit plaintext block to a -bit ciphertext block, with the exact mapping determined by the cipher design and selected key. The mapping can be viewed as a lookup table.
Figure 7.5 is an example of a 2-bit ideal block cipher. The table shows input plaintext blocks in the left column, different keys in the top row, and the resulting output ciphertext block in the body of the table. To be used for sending a confidential message, both the sender and receiver would know the table (e.g. stored in memory on their devices), or some way to calculate the table) and agree upon the key to use. For a given plaintext block, the sender looks up the key to find the output ciphertext to send. The receiver looks up the receiver ciphertext in the column of the key, and the row determines the plaintext.
Exercise 7.1 (Encrypt with Ideal Cipher 1). Encrypt the message Tokyo using the above ideal 2-bit block cipher 1 with key K6.
Solution 7.1 (Encrypt with Ideal Cipher 1). As the example block cipher operates on 2-bit binary blocks, but a five letter English message is to be encrypted we will make assumptions about the encoding and mode of operation to be used.
First, we will assume ASCII (or UTF-8) encoding is to be used (see Section B.1.4). Each letter will map to an 8-bit value, i.e. T = 01010100, o = 01101111, k = 01101011, and y = 01111001. The resulting plaintext in binary is 40 bits:
0101010001101111011010110111100101101111
Second, as we have 40 bits of plaintext, but a 2-bit block cipher, we will assume each 2-bit block of plaintext will be encrypted (20 blocks in total), and the resulting 20 ciphertext blocks will be concatenated to produce final 40 bit ciphertext. This naive approach is referred to as the Electronic Code Book mode of operation. Modes of operations are discussed in Chapter 11. The 20 plaintext blocks are:
01 01 01 00 01 10 11 11 01 10 10 11 01 11 10 01 01 10 11 11
Consider the 1st plaintext block of 01, using key K6, looking up the block cipher table returns a ciphertext block of 10. We know have the first of 20 ciphertext blocks and can move on to the 2nd ciphertext block. It turns out the next plaintext block is the same as the first (01), and since the same key is used (K6), the same ciphertext block will be output (10). In fact, the first three plaintext blocks are the same, so the ciphertext blocks so far are:
10 10 10
The 4th plaintext block is 00. Looking up in the table with key K6 produces output ciphertext block 11. We know have:
10 10 10 11
Continuing with all 20 plaintext blocks will produce ciphertext blocks:
10 10 10 11 10 00 01 01 10 00 00 01 10 01 00 10 10 00 01 01
Concatenating all ciphertext blocks together produces the ciphertext:
1010101110000101100000011001001010000101
Should the ciphertext be encoded as ASCII/UTF8 to complete the encryption? It could be, but note that some of the characters may note be printable (e.g. ESCape or ACK). For block ciphers we typically operate on binary plaintext and ciphertext. Encoding and decoding between binary and other formats is not normally part of the cipher, so we will leave the ciphertext as a sequence of bits.
The above exercise identified several issues that arise when applying an ideal block cipher:
- Encoding/decoding: independent of block cipher, which operate only in binary values
- Mode of operation: typically independent of block cipher, which operate only on a single block
- Repetition of plaintext blocks: undesirable. Make block size larger and use mode of operation that obscures repetition
- Key space: larger block size needed to allow more keys in ideal block cipher
- Implementing an ideal block cipher: how are they generated? can all values be stored?
The following questions will explore some of these issues further.
Figure 7.6 shows a different 2-bit ideal block cipher. It maps plaintext to ciphertext in a different order than cipher 1.
This example is just used for illustrative purposes. If you had an ideal block cipher that covered every permutation of plaintext values, then only a single cipher is needed.
Question 7.1 (What is plaintext with key K13, ciphertext 11 with ideal cipher 2?). What is plaintext with key K13, ciphertext 11 with ideal cipher 2?
Decryption also involves a lookup. In the column for key K13, identify the ciphertext 11, and the row indicates the original plaintext 10.
Question 7.2 (What is plaintext with key K4, ciphertext 11 with ideal cipher 2?). What is plaintext with key K4, ciphertext 11 with ideal cipher 2?
Same cipher, same ciphertext but different key. However in column of K4 there are two values of ciphertext 11. So we cannot determine for sure what was the original plaintext: 00 or 10. This actually is a trick question, since the cipher design is in error. A cipher must be reversible, so decryption is possible. This is an example of a cipher design error that includes an irreversible mapping.
Figure 7.7 shows the fixed cipher: it is now reversible, and decryption is possible for all values of key and ciphertext.
Question 7.3 (How many bits are needed to represent the key in cipher 2?). The example 2-bit ideal block cipher 2 (as well as cipher 1) list 24 different keys (or mappings from plaintext to ciphertext). How many bits are needed to represent a key for this cipher?
Firstly, why are 24 keys listed? With a 2-bit block, there are possible blocks, i.e. 00, 01, 10, and 11. There are different ways to arrange those 4 plaintext blocks to produce ciphertext, i.e. 24 permutations of the plaintext blocks. A key is used to select the distinct permutation.
With key length of 1 bit, we can represent possible keys. With a key length of 2 bits, we can represent possible keys. With a key length of 3 bits, we can represent possible keys. With a key length of 4 bits, we can represent possible keys. With a key length of 5 bits, we can represent possible keys. That is, a key length of 4 bits is not enough to represent our 24 keys, but a key length of 5 is. Therefore we need a 5-bit key for this ideal 2-bit block cipher.
Question 7.4 (How to reduce repetition of plaintext blocks?). With a 2-bit ideal block cipher, with a long plaintext, many of plaintext blocks will repeat. This is bad for security (see Modes of Operation). What can you change in the design of an ideal block cipher that reduces repetition of plaintext blocks?
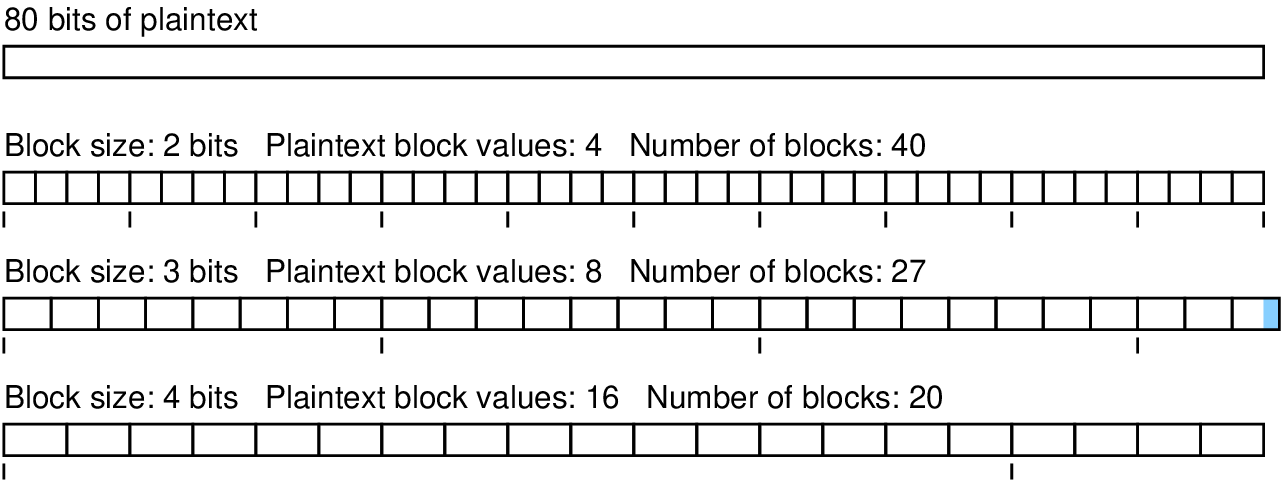
Increasing the block size for a block cipher will reduce the change of block repetition. Recall the first example of the 2-bit ideal block cipher encrypting Tokyo. The plaintext was 40-bits, resulting in 20 blocks. As there are only different plaintext values, there will be repetition. On average (if the plaintext was random, which is not likely but it simplifies the analysis), each plaintext value will be repeated times.
If however a 3-bit ideal block cipher was used, there would be different plaintext values. There would be 14 blocks (, with the last block having just 1 bit of plaintext). On average, each plaintext value will be repeated , which is less than 2 times.
Increasing to a 4-bit ideal block cipher gives 16 different plaintext values, 10 blocks, and a possibility there will be no repetition. Of course if the plaintext is much longer than 40 bits, then repetition is still likely.
Figure 7.8 illustrates the impact of different block sizes for an example 80 bit plaintext (whereas the previous example was a 40 bit plaintext).
Note that with a block size of 3 bits, the last block contains 2 bits of plaintext and 1 bit of padding. Padding is needed as all blocks must be the same size (since block ciphers operate on fixed sized blocks). There are different schemes for padding, e.g. bit padding, zero padding and PKCS7.
- -bit block cipher takes bit plaintext and produces bit ciphertext
- possible different plaintext blocks
- Encryption must be reversible (decryption possible)
- Number of permutations of plaintext (and number of keys) is
- Design trade-offs:
- Large block size to reduce plaintext repetitions (64-bits is good)
- Key space large enough to avoid brute force, but small enough to make distribution practical
- Small block size to simplify implementation
The trade-offs are conflicting, meaning ideal block ciphers are good in theory, but in practice we need a different design approach.
Exercise 7.2 (Ideal 64-bit Block Cipher). Consider an ideal 64-bit block cipher. How many different different keys are possible? How many bits are needed to store a single key? How much space is required to store the mappings?
Solution 7.2 (Ideal 64-bit Block Cipher). We will not attempt to list all keys. With 64-bit blocks, there are different permutations or mappings, meaning possible keys. To store a single key, we need about bits. Our software calculator will not handle this, not even bc. So let’s try Wolfram Alpha, which returns . That means about bits are needed to store a key. That is approximately 125,000,000 TB. If someone wanted to send a short encrypted message to you, they would first need to exchange a 125,000,000 TB key with you. Hence we see an ideal block cipher with large blocks is not practical due to the key length.
For storage of the mappings, consider if you had to create a table similar to the 2-bit ideal block ciphers. There are columns, representing the keys. There are rows, representing the possible plaintext values. Each cell in the table contains a 64-bit, or 8 Byte, ciphertext value. So the storage space needed is Bytes. If you attempt to calculate this you will quickly see it is not practical to store the entire table.
Video: Ideal Block Cipher (8 min; Mar 2021)
To overcome the limitations of ideal block ciphers, Horst Feistel designed a general scheme that is practical in the sense of implementation and key lengths, but still achieves suitable security.
- Ideal block ciphers are not practical
- Feistel proposed applying two or more simple ciphers in sequence so final result is cryptographically stronger than component ciphers
- -bit block length; -bit key length; transformations
- Feistel cipher alternates: substitutions, transpositions (permutations)
- Applies concepts of diffusion and confusion
- Applied in many ciphers today
- Approach:
- Plaintext split into halves
- Subkeys (or round keys) generated from key
- Round function, , applied to right half
- Apply substitution on left half using XOR
- Apply permutation: interchange to halves
For example, with a 64-bit block cipher, there are possible mappings/keys, meaning the key length is bits.
- Diffusion
- Statistical nature of plaintext is reduced in ciphertext
- E.g. A plaintext letter affects the value of many ciphertext letters
- How: repeatedly apply permutation (transposition) to data, and then apply function
- Confusion
- Make relationship between ciphertext and key as complex as possible
- Even if attacker can find some statistical characteristics of ciphertext, still hard to find key
- How: apply complex (non-linear) substitution algorithm
Diffusion and confusion are concepts introduced by Claude Shannon. See a summary of Shannon’s contributions in telecommunications, digital circuits and cryptography in Chapter C.
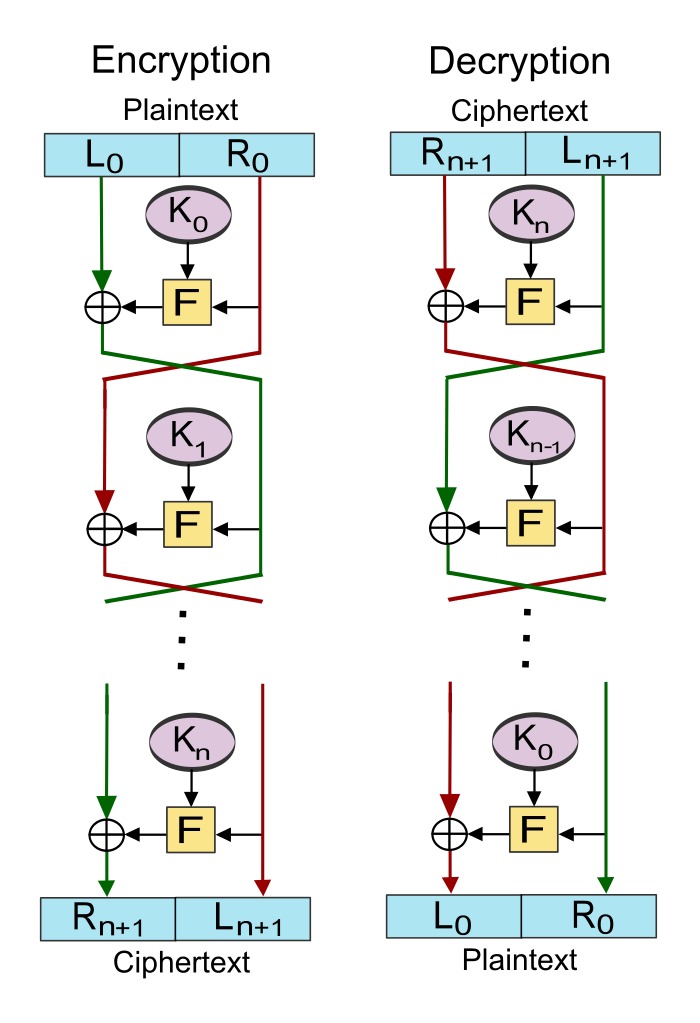
Credit: Amirki, https://commons.wikimedia.org/wiki/File:Feistel_cipher_diagram_en.svg, CC BY-SA 3.0
You don’t need to know the details of the Feistel structure. Just be aware that it is a design principle used in many block ciphers, including DES.
- Exact implementation depends on various design features
- Block size, e.g. 64, 128 bits: larger values leads to more diffusion
- Key size, e.g. 128 bits: larger values leads to more confusion, resistance against brute force
- Number of rounds, e.g. 16 rounds
- Subkey generation algorithm: should be complex
- Round function : should be complex
- Other factors include fast encryption in software and ease of analysis
- Trade-off: security vs performance
Video: Ideal Block Cipher vs Feistel Structure (2 min; Mar 2021)
7.4 Stream Cipher Design Principles
Stream ciphers were designed to be fast using an XOR operation, and usually encrypt a bit or byte at a time.
- Encrypts a digital data stream one bit or one byte at a time
- One time pad is example; but practical limitations
- Typical approach for stream cipher:
- Key () used as input to bit-stream generator algorithm
- Algorithm generates cryptographic bit stream () used to encrypt plaintext
- is XORed with each byte of plaintext
- Users share a key; use it to generate keystream
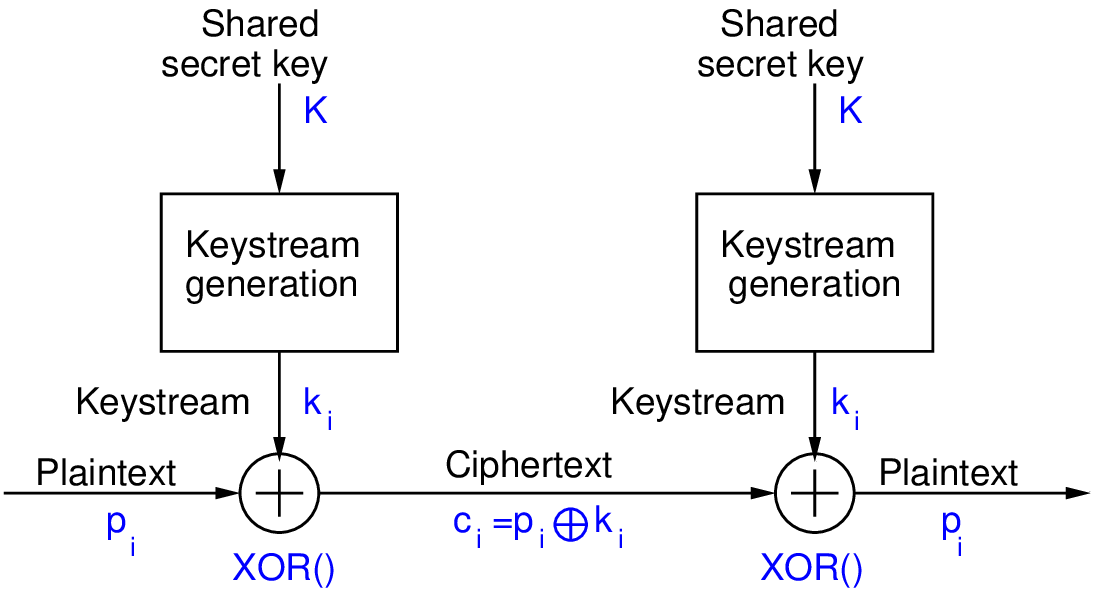
Figure 7.10 illustrates the general operation of a stream cipher encryption and decryption. The sender uses a shared secret key and an algorithm to generate effectively a random stream of bits. This random stream of bits is XORed with the plaintext bits as needed.
The receiver uses the same key and algorithm, which in turn generates the same random stream of bits. When XORed with the ciphertext, the original plaintext is output.
An issue when using stream ciphers is that a key cannot be re-used. This is usually addressed by introducing an initialisation value or vector (IV).
- Encrypting two different plaintexts with the same key leads to key re-use attack
- Attacker intercepts two ciphertexts: and
- Properties of XOR: commutative and
- Attacker performs XOR on two ciphertexts
- Even without knowing or , attacker can easily use frequency analysis to discover both
- Solution: Use additional IV that changes for every encryption
Question 7.5 (When can key re-use attack be successful if IV is used?). If a stream cipher is using a -bit Initialisation Vector/Value (IV), but the same key, under what conditions is a key re-use attack possible? Assume the IV increments every time an encrypt operation is performed.
7.5 Example: Brute Force on DES
Now let’s consider an example of brute force on a real cipher, DES.
- DES is 64-bit block cipher with 56-bit (effective) key length
- Developed in 1977, recommended standard until 1990’s
- Brute force: operations
- Hardware built to perform brute force attack
- 1998: DeepCrack
- 2006: COPACABANA
In 1998, the Electronics Frontiers Foundation (EFF) developed DeepCrack to demonstrate how insecure DES was.
- Developed by EFF
- Cost less than $US250,000
- keys/sec
- Solved DES challenge in 56 hours
- See www.cryptography.com and www.eff.org

Credit: Wikimedia, CC0 1.0 Public Domain https://commons.wikimedia.org/wiki/File:Paul_kocher_deepcrack.jpg
Figure 7.11: Paul Kocher and DeepCrack
Video: DeepCrack Brute Force on DES (1 min; Mar 2021)
In 2006, as a demonstration of their hardware, SciEngines developed COPACABANA.
- Joint effort by SciEngines and German universities
- 120 Field Programmable Gate Arrays (FPGAs), keys/sec/FPGA
- For comparison, a Pentium 4: keys/sec
- Brute force DES in 8.6 days
- Cost about $US10,000
- See www.sciengines.com
Using the above example, we can roughly estimate what it would cost today to brute force DES.
- Moore’s law: computers double speed every 1.5 years
- Alternative: computers halve in cost every 1.5 years
- $US10,000 to brute force DES in 2006
- Cost has halved about 10 times
- Cost to brute force DES in 2020: $10
A simplification of Moore’s law is that computers double their speed every 1.5 years. In practice it is not that simple, but it is a useful rule to estimate the cost of brute force today. It means in 1.5 years time, you could buy a computer that double the speed if a new computer today, and at the same cost. Alternatively, you could buy a lower specced computer, which is the same speed as a new computer today, buy half the cost of today’s computer.
Assuming computers halve in cost every 1.5 years, between 2006 and 2020 is 14 years. Over 15 years, there are 10 1.5 year periods, so the cost would halve 10 times. (Again since this is an estimate, let’s use 15 years instead of 14). If you half $10,000 10 times, you get $9.76. That is, a $10 computer today can brute force DES in 8.6 days.
As brute force attacks can be parallelised easily, you could spend $100 on 10 computers (or buy a $100 computer) and break DES in less than a day. DES is not secure against a brute force attack (and hasn’t been for a long time).
Video: SciEngines Copacabana Brute Force on DES (3 min; Mar 2021)
7.6 Example: Brute Force on AES
Another demonstration of hardware brute force capabilities was again given by SciEngines in 2013, this time attacking AES.
- Rivyera S3 supported up to 128 Xilinx Spartan-3 FPGAs
- Approx $100 per FPGA (XCS5000)
- AES-128 Brute Force
- keys per sec
- keys per mW
- Biclique Attack
- keys per sec
- keys per mW
FPGAs are essentially computer processors programmed for a specific task, in this case, decrypting with AES very fast. For about $12,800 a RIVYERA could decrypt AES-128 at a rate of keys per second.
A known plaintext attack on AES is called the Biclique attack. The RIVYERA implementation of the Biclique attack could decrypted AES-128 at a rate of keys per sec, about twice that of a brute force.
Now let’s consider what it would take to break AES.
- AES-128 has key space of
- 2013: $US12,800 for k/s
- Assume: computers double speed every 1.5 years
- 2020: Increase by ;
k/s
- $12,800: years
- $12,800,000: years
- $12,800,000,000: years
- Biclique attack about 2 to 4 times faster, but requires known plaintext/ciphertext pairs
- In 2035, cost $12,800,000,000 to brute force AES-128 in 670,000,000,000 years
Applying the same logic from analysis of DES brute force and Moore’s law (i.e. every 1.5 years halve cost or double speed), we can perform a rough analysis of the cost/time to break AES-128. The numbers (dollars, years) are so large such that even if the approximations are incorrect by a factor of 1,000,000,000 (e.g. reducing years to years, then it is still impossible to break AES-128.
Video: SciEngines Rivyera Attack on AES (4 min; Mar 2021)
7.7 Example: Meet-in-the-Middle Attack
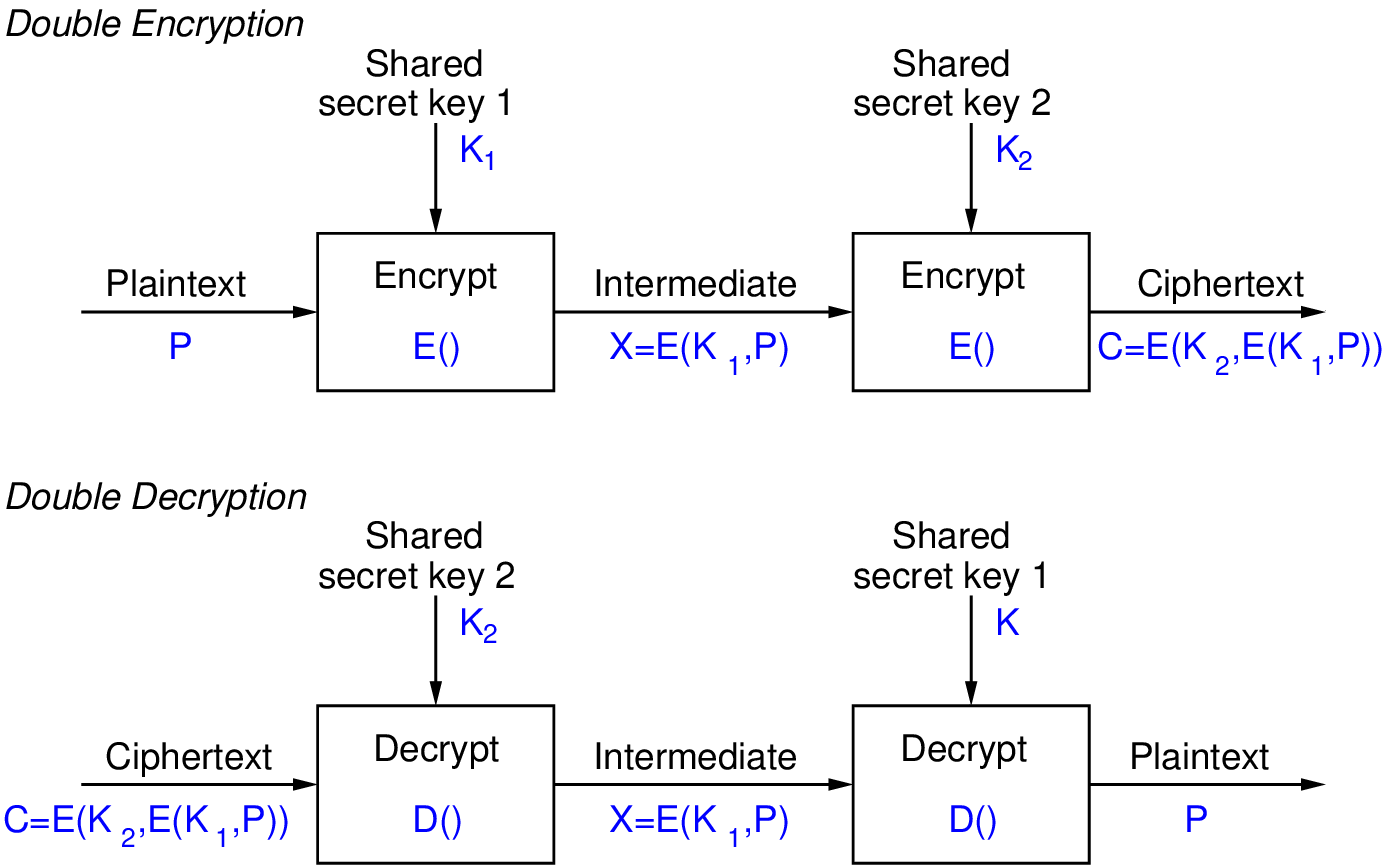
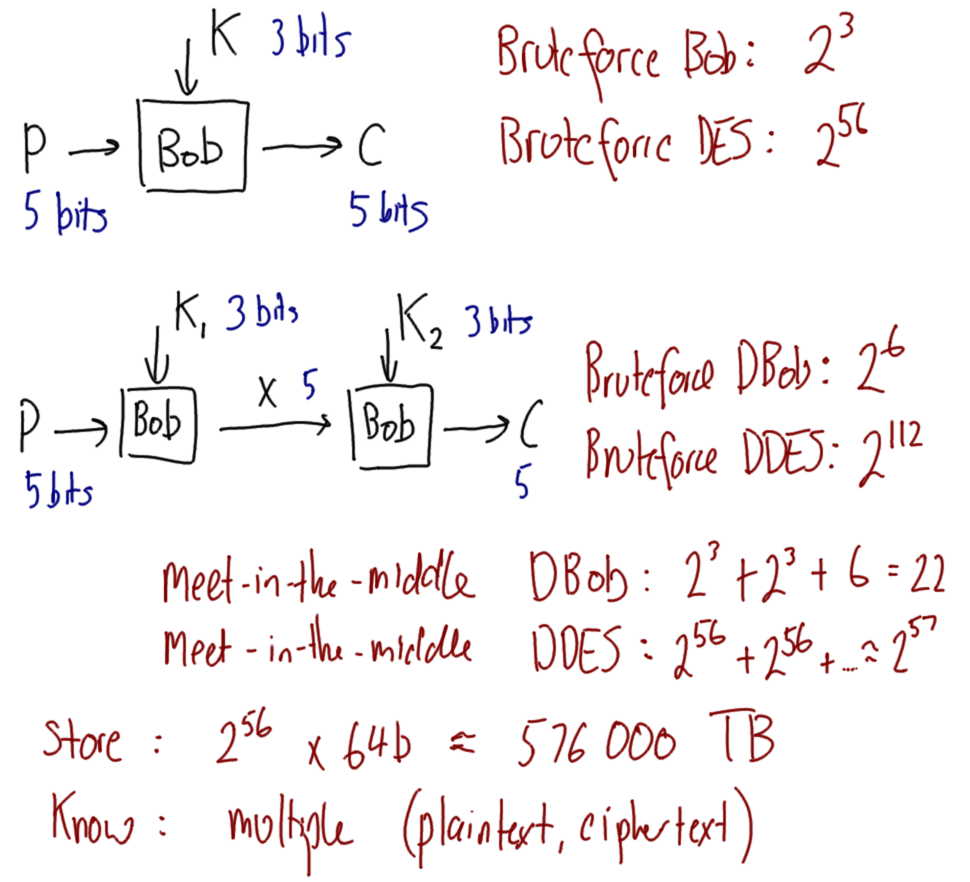
One way to increase the key length of a block cipher is to apply the cipher multiple times, each time using a different key. Applying the cipher twice is referred to as double encryption.
- Encrypt plaintext with one key, then encrypt output with another key
- Advantage: doubles the key length
- Single version of cipher has -bit key
- Double version of cipher uses two different -bit keys
- Worst case brute force:
- Advantage: uses an existing cipher
- Disadvantage: doubles the processing time
- Problem: double encryption is subject to meet-in-the-middle attack
Double encryption was a (naive) option for extending the key length of DES. It effectively would double the key length from 56 bits to 112 bits. A new cipher would not have to be designed or analysed, and existing software/hardware implementations could be used.
But a meet-in-the-middle attack makes Double-DES (or double encryption on any block cipher) insecure.
- Double Encryption where key is -bits:
- Say
- Attacker knows two plaintext, ciphertext pairs
and
- Encrypt using all values of to get multiple values of
- Store results in table and sort by
- Decrypt using all values of
- As each decryption result produced, check against table
- If match, check current on . If obtained, then accept the keys
- With two known plaintext, ciphertext pairs, probability of successful attack is almost 1
- Encrypt/decrypt operations required: (twice as many as single encryption)
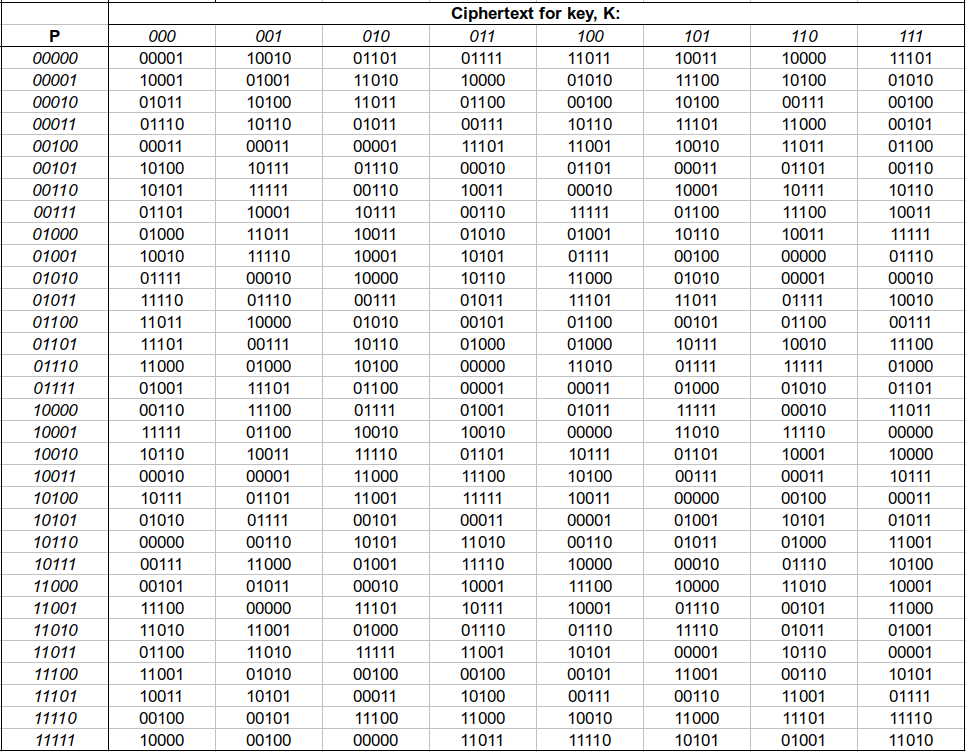
Figure 7.15 shows an example 5-bit block cipher with a 3-bit key. To encrypt, look in the left column to find the row of the plaintext, then look for the column corresponding to the key. The intersection of row and column gives the ciphertext.
This example block cipher is used in the Meet-in-the-Middle attack exercise.
Exercise 7.3 (Meet-in-the-Middle Attack). Figure 7.15 shows an example 5-bit block cipher, referred to as Bob’s Cipher. A double version of Bob’s cipher, called Double-Bob, was used by two users to exchange multiple encrypted messages using the same 6-bit secret key. You have obtained the plaintext/ciphertext pairs of two of those messages: and . Using a meet-in-the-middle attack, find the secret key.
Solution 7.3 (Meet-in-the-Middle Attack). Figure 7.16 shows notes on performing the attack. Figure 7.17 shows calculations of the performance of the attack, and compares to an attack on Double-DES.
Video: Meet-in-the-Middle attack on 5-bit block cipher (52 min; Feb 2016)
- Different variations:
- Use 2 keys, e.g. Triple-DES 112 bits
- Use 3 keys, e.g. Triple-DES 168 bits
- Why E-D-E? To be compatible with single DES:
- Problem: 3 times slower than single DES
Figure 7.18 shows the concept of Triple Encryption, where two different keys are used. This effectively doubles the key strength compared to the original cipher. Another variation (not shown) would be to use three different keys, effectively tripling the key strength.
Note that if you use the same key for each step, then because of the E-D-E approach, this reverts to the original cipher. That is, if you use Triple-DES but use the same key in each step, this reverts to (single) DES. The benefit of this is that you can have an implementation of Triple-DES (which is built on the implementations of DES), and allow the user to choose a key to suit their needs: 1 key for DES, 2 keys for 112-bit security, 3 keys for 168-bit security.
7.8 Example: Cryptanalysis on Triple-DES and AES
Table 7.2 compares cryptanalysis on Triple-DES and AES against brute force attacks.
| Cipher | Method | Key | Required resources:
| ||
| space | Time | Memory | Known data | ||
| DES | Brute force | - | - | ||
| 3DES | MITM | ||||
| 3DES | Lucks | ||||
| AES 128 | Biclique | ||||
| AES 256 | Biclique | ||||
- Known data: chosen pairs of (plaintext, ciphertext)
- Lucks: S. Lucks, Attacking Triple Encryption, in Fast Software Encryption, Springer, 1998
- Biclique: Bogdanov, Khovratovich and Rechberger, Biclique Cryptanalysis of the Full AES, in ASIACRYPT2011, Springer, 2011
Video: Theoretical Attacks on DES and AES (2 min; Mar 2021)