Appendix B
Data Formats
File: crypto/formats.tex, r1766
Information that is to be secured can be represented in a variety of data formats. In this chapter we list key data formats used throughout the book, and more generally in cryptography. We demonstrate tools for manipulating the data.
B.1 Common Data Formats
B.1.1 English Alphabet
A character set of the 26 letters in the English alphabet:
a b c d e f g h i j k l m n o p q r s t u v w x y z
Unless otherwise stated, case insensitive. A case sensitive variation would have 52 characters in the set. Other variations are possible, where additional characters are included (e.g. digits, punctuation) or different languages are used.
Alphabetical ordering is used, and often the letters are mapped to integers, starting at a = 0.
Primarily seen in classical ciphers.
B.1.2 Printable Keyboard Characters
A character set consisting of the characters printable from the keys on a typical keyboard. On US/English keyboards, usually 94 characters:
- 26 uppercase English letters
- 26 lowercase English letters
- 10 digits
- 32 punctuation characters (see your keyboard)
Keys such as SPACE, TAB and ENTER are usually not considered printable.
Primarily seen in applications dealing with user input, e.g. passwords.
B.1.3 Binary Data
In modern systems, all data is represented as binary values. This includes text, documents, images, applications, audio and video. There are different encodings to map these data into binary (some of which are described in this chapter).
In this book, when referring to sequence of bits, the 1st bit refers to the left most bit in the sequence. (In some cases, bits are indexed starting at 0, e.g. the 0th bit, the 1st bit; it is made clear when this is the case). For example, for the sequence 01001111, the 1st bit is 0, the 2nd bit is 1, the 3rd bit is 0 and the last (8th) bit is 1. Also, the most significant bit is the left most bit. In the previous example, the 2nd bit has the decimal value of 64, and the last (8th) has the decimal value of 1.
Note that encoding and decoding is not equivalent to encryption and decryption. That is, encoding (from say ASCII to Base64) does not provide any significant security value as there is not key involved. Even if an attacker did not know the encoding used, they could easily try all possible encodings.
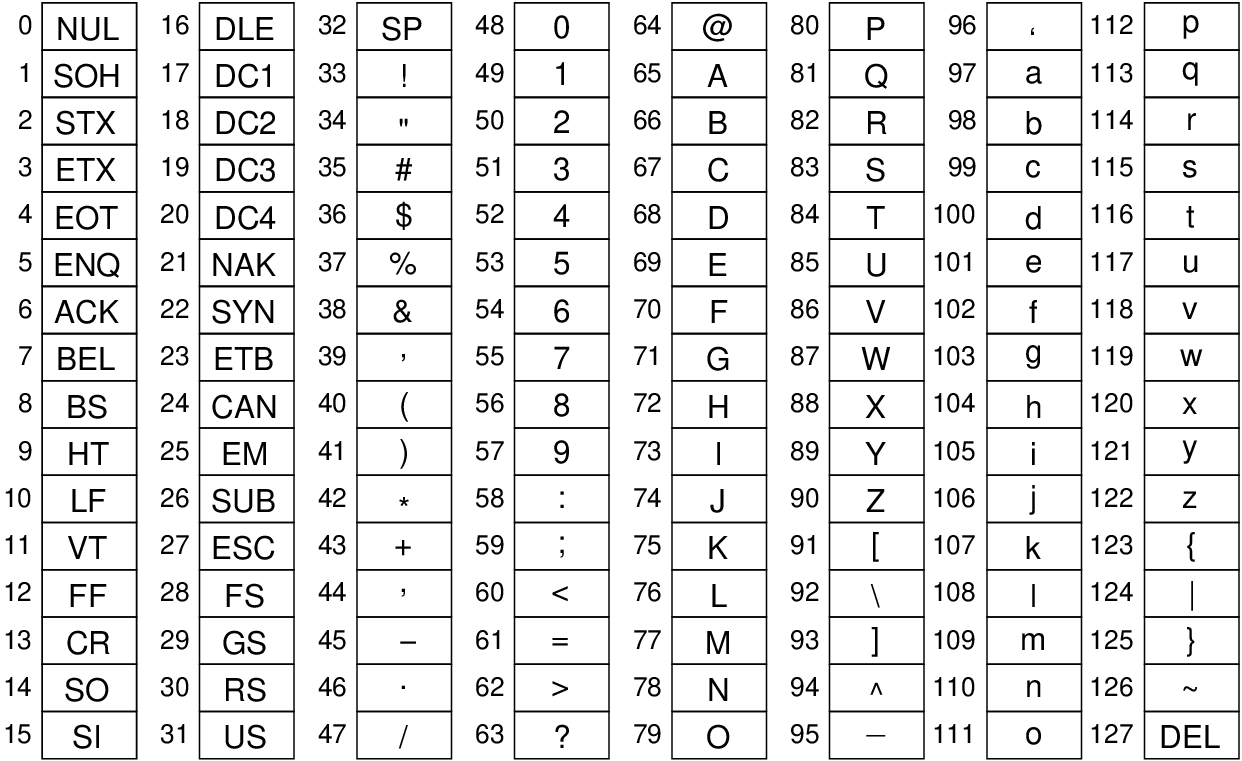
B.1.4 ASCII
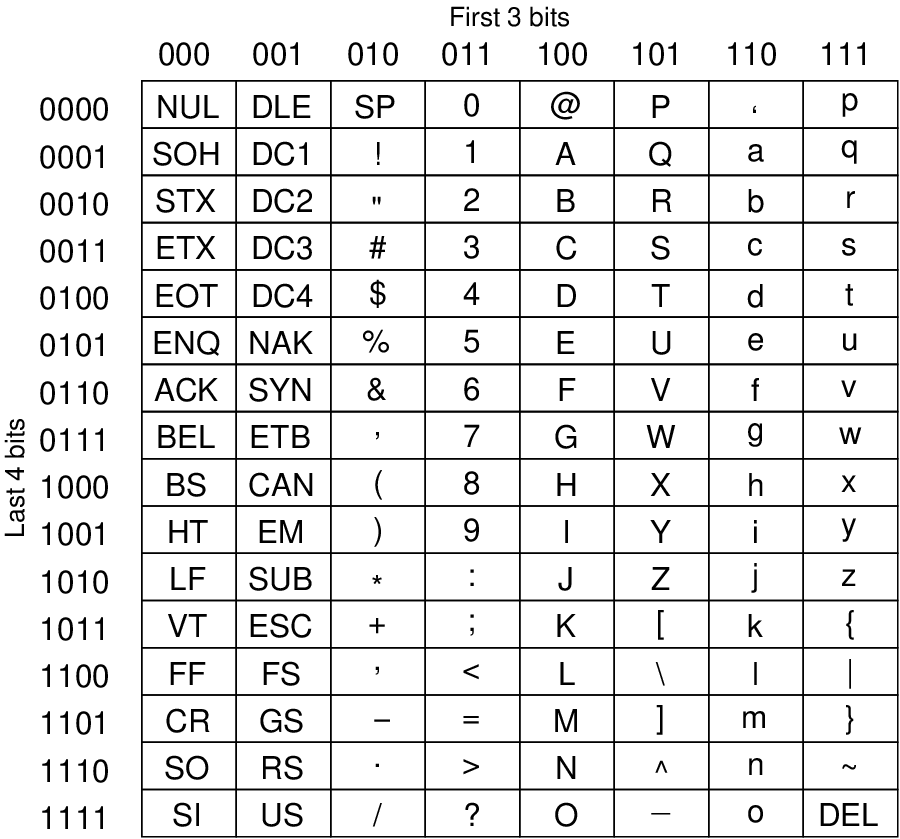
American Standard Code for Information Interchange (ASCII) is a common standard for representing keyboard/computer characters in a digital format. Also referred to as the International Reference Alphabet and a subset of Unicode, there are 128 characters in the ASCII character set. Section B.1 shows the mappings to decimal values, while Section B.2 shows the mapping to 7-bit binary values (take the 3 bits from the column and then the 4 bits from the row).
While ASCII can be represented in 7-bits, it is commonly used in computer files as 8-bit values, where the 1st bit is always a binary 0. For example, uppercase A is binary 01000001.
Ordering is by the numerical value, e.g. ! comes before A, which comes before a.
You can see the standard 94 printable keyboard characters from ! through to ˜.
B.1.5 Hexadecimal
A character set with 16 characters:
0 1 2 3 4 5 6 7 8 9 A B C D E F
When communicating binary data (to humans), it is sometimes represented in hexadecimal as it uses four times less characters (4 bits per character), and has less chance of reading/writing errors.
Examples of using hexadecimal to illustrate binary data includes: secret keys, public key pair values, very large numbers (e.g. large primes), ciphertext, and addresses.
B.1.6 Base64
An alternative to hexadecimal representation of binary data is using Base64 encoding. Base64 is a character set of 64 characters:
- 26 uppercase English letters
- 26 lowercase English letters
- 10 digits
- 2 punctuation characters which are + and /
The = character is used to indicate padding (and is not part of the 64 characters). See online resources for an explanation of padding.
Base64 maps 6 bits to a character and therefore is more concise than hexadecimal. It is often used when communicating binary data in text-based protocols in networks (e.g. including binary data in a HTML page or email).
B.2 Conversions using Linux
In Linux, xxd is useful for viewing text files (containing ASCII) in binary and hexadecimal. See Section 3.1.1.
For Base64, the command base64 can be used:
$ echo -n "This is a message." > data.txt
$ xxd data.txt
00000000: 5468 6973 2069 7320 6120 6d65 7373 6167 This is a messag
00000010: 652e e.
$ base64 data.txt
VGhpcyBpcyBhIG1lc3NhZ2Uu
$ base64 data.txt > data.b64
$ base64 -d data.b64
This is a message.$
To convert ASCII characters to their decimal value, in a Linux Bash terminal you can use printf (newlines have been added below to make the output clearer):
$ printf '%d' "'A"
65
$ printf '%d' "'a"
97
$ printf '%d' "'!"
33
$ printf '%d' "'~"
126
It is a little more cumbersome in the opposite direction:
$ printf "\\$(printf '%03o' "65")"
A
$ printf "\\$(printf '%03o' "97")"
a
$ printf "\\$(printf '%03o' "33")"
!
$ printf "\\$(printf '%03o' "126")"
~
You are advised to simply lookup the table or find another tool, rather than use the Bash commands as above.
B.3 Conversions using Python
There are different ways to convert between varying formats in Python. The following code shows some examples. The code is also available in the Steve’s Workshops GitHub repository. The code below is version 4c0faec. An example of the output from running the conversion functions follows the code.
[Demonstration of converting between different formats in Python]
'
Convert data between different formats. No (or very little) error checking
is performed. You need to make sure the input data for the conversion is
in the format specified.
'
import base64
import logging
logger = logging.getLogger("Conversions")
def bytes_to_text(b):
return b.decode('utf-8')
def text_to_bytes(s):
return s.encode('utf-8')
def bytes_to_base64(b):
return bytes_to_text(base64.b64encode(b))
def base64_to_bytes(b64):
return base64.b64decode(b64)
def bytes_to_hex(b):
return b.hex()
def hex_to_bytes(h):
return bytes.fromhex(h)
def base64_to_text(b64):
return bytes_to_text(base64_to_bytes(b64))
def base64_to_hex(b64):
return bytes_to_hex(base64_to_bytes(b64))
def text_to_base64(s):
return bytes_to_base64(text_to_bytes(s))
def hex_to_base64(h):
return bytes_to_base64(hex_to_bytes(h))
def text_to_hex(s):
return bytes_to_hex(text_to_bytes(s))
def hex_to_text(h):
return bytes_to_text(hex_to_bytes(h))
def text_to_list(s):
return list(s)
def list_to_text(l):
return "".join(l)
def hex_to_binary(h):
return bin(int(h,16))[2:]
def binary_to_hex(bi):
return hex(int(bi,2))[2:]
def binary_to_bytes(bi):
return hex_to_bytes(binary_to_hex(bi))
def bytes_to_binary(b):
return hex_to_binary(bytes_to_hex(b))
def text_to_binary(s):
return bytes_to_binary(text_to_bytes(s))
def binary_to_text(bi):
return bytes_to_text(binary_to_bytes(bi))
def base64_to_binary(b64):
return bytes_to_binary(base64_to_bytes(b64))
def binary_to_base64(bi):
return bytes_to_base64(binary_to_bytes(bi))
def letter_to_number(c, charset="lowercase"):
'
Convert a single character into a number
Converts a -> 0, b -> 1, c -> 2, ... or
if uppercase A -> 0, B -> 1, C -> 2, ...
'
if charset == "uppercase":
return ord(c) - 65
else:
return ord(c) - 97
def number_to_letter(n, charset="lowercase"):
'
Convert a number into a single character
See char_to_num(c) - this is the opposite
'
if charset == "uppercase":
return chr(n + 65)
else:
return chr(n + 97)
def text_to_numbers(text, charset="lowecase"):
'
Convert a string into a list of numbers
:Example:
- input: str = "abc"
- output: list = [0, 1, 2]
'
return [letter_to_number(c, charset) for c in text]
def numbers_to_text(nums, charset="lowercase"):
'
Convert a list of numbers into a string
See text_to_nums(text) - this is the opposite
'
return .join([num_to_char(n, charset) for n in nums])
if __name__=='__main__':
import sys
import argparse
# Process command line arguments
parser = argparse.ArgumentParser(
description="Convert between different formats for cryptography",
formatter_class=argparse.RawDescriptionHelpFormatter,
epilog='
example (command-line):
$ python conversions.py
')
parser.add_argument("-l", "--log",
choices=["DEBUG", "INFO", "WARNING", "ERROR", "CRITICAL"])
args = parser.parse_args()
# Enable logging based on command line input
if args.log is None:
numeric_log_level = logging.ERROR
else:
numeric_log_level = getattr(logging, args.log.upper(), None)
if not isinstance(numeric_log_level, int):
raise ValueError('Invalid log level: %s' % args.log)
logging.basicConfig(level=numeric_log_level)
data1_str = "Hello"
data1_bytes = text_to_bytes(data1_str)
data1_b64 = text_to_base64(data1_str)
data1_hex = text_to_hex(data1_str)
data1_bin = text_to_binary(data1_str)
data1_list = text_to_list(data1_str)
print("Converting Text to ...")
print(" Text:" + str(data1_str))
print(" Bytes :" + str(data1_bytes))
print(" Base64:" + str(data1_b64))
print(" Hex :" + str(data1_hex))
print(" Binary:" + str(data1_bin))
print(" List :" + str(data1_list))
data2_b64 = "SGVsbG8="
data2_bytes = base64_to_bytes(data2_b64)
data2_str = base64_to_text(data2_b64)
data2_hex = base64_to_hex(data2_b64)
data2_bin = base64_to_binary(data2_b64)
print("Converting Base64 to ...")
print(" Text:" + str(data2_str))
print(" Bytes :" + str(data2_bytes))
print(" Base64:" + str(data2_b64))
print(" Hex :" + str(data2_hex))
print(" Binary:" + str(data2_bin))
data3_hex = "48656c6c6f"
data3_bytes = hex_to_bytes(data3_hex)
data3_str = hex_to_text(data3_hex)
data3_b64= hex_to_base64(data3_hex)
data3_bin = hex_to_binary(data3_hex)
print("Converting Hex to ...")
print(" Text:" + str(data3_str))
print(" Bytes :" + str(data3_bytes))
print(" Base64:" + str(data3_b64))
print(" Hex :" + str(data3_hex))
print(" Binary:" + str(data3_bin))
data4_chr = 'c'
data4_num = letter_to_number(data4_chr)
data5_str = "hello"
data5_nums = text_to_numbers(data5_str)
print("Letter " + data4_chr + " is " + str(data4_num))
print("Text " + data5_str + " is " + str(data5_nums))
sgordon@chilli:~/git/workshops/python/demos$ python3 conversions.py
Converting Text to ...
Text:Hello
Bytes :b'Hello'
Base64:SGVsbG8=
Hex :48656c6c6f
Binary:100100001100101011011000110110001101111
List :['H', 'e', 'l', 'l', 'o']
Converting Base64 to ...
Text:Hello
Bytes :b'Hello'
Base64:SGVsbG8=
Hex :48656c6c6f
Binary:100100001100101011011000110110001101111
Converting Hex to ...
Text:Hello
Bytes :b'Hello'
Base64:SGVsbG8=
Hex :48656c6c6f
Binary:100100001100101011011000110110001101111
Letter c is 2
Text hello is [7, 4, 11, 11, 14]