6 Classical Ciphers

Chapter 6
Classical Ciphers

6.1 Caesar Cipher
  6.1.1 Caesar Cipher Definitions and Examples
  6.1.2 Brute Force Attack on Caesar Cipher
6.2 Monoalphabetic Ciphers
  6.2.1 Monoalphabetic Cipher Definitions and Examples
  6.2.2 Brute Force Attack on Monoalphabetic Cipher
  6.2.3 Frequency Analysis Attack on Monoalphabetic Cipher
6.3 Playfair Cipher
6.4 Polyalphabetic Ciphers
6.5 Vigenère Cipher
6.6 Vernam Cipher
6.7 One Time Pad
6.8 Transposition Techniques

File: crypto/classical.tex, r1964

This chapter introduces several historical or classical ciphers. While these ciphers are no longer used, they are simple enough to perform operations by hand while demonstrating important concepts used in the design of most symmetrical ciphers used today. The actual history of the ciphers is not presented here; you can find that in most cryptography textbooks or via searches online.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

6.1 Caesar Cipher

6.1.1 Caesar Cipher Definitions and Examples

Algorithm 6.1 (Caesar Cipher). To encrypt with a key k, shift each letter of the plaintext k positions to the right in the alphabet, wrapping back to the start of the alphabet if necessary. To decrypt, shift each letter of the ciphertext k positions to the left (wrapping if necessary).

In the examples we will assume the Caesar cipher (and most other classical ciphers) operate on case-insenstive English plaintext. That is, the character set is a through to z. However it can also be applied to any language or character set, so long as the character set is agreed upon by the users.

Exercise 6.1 (Caesar Cipher Encryption). Using the Caesar cipher, encrypt plaintext hello with key 3.

Solution 6.1 (Caesar Cipher Encryption). To encrypt the plaintext hello with the key 3, each letter in the plaintext is encrypted by shifting 3 positions to the right in the alphabet. The letter 3 positions to the right of h is K, as illustrated below:

a b c d e f g h i j K l m n o p q r s t u v w x y z

The letter 3 positions to the right of e is H:

a b c d e f g H i j k l m n o p q r s t u v w x y z

The letter 3 positions to the right of l is O (notin that there are two l’s in the plaintext, so there will be two O’s in the ciphertext):

a b c d e f g h i j k l m n O p q r s t u v w x y z

The letter 3 positions to the right of o is R:

a b c d e f g h i j k l m n o p q R s t u v w x y z

The final ciphertext is therefore KHOOR.

Video: Caesar Cipher Encryption Example (2 min; Feb 2020)

Question 6.1 (How many keys are possible in the Caesar cipher?). If the Caesar cipher is operating on the characters a–z, then how many possible keys are there? Is a key of 0 possible? Is it a good choice? What about a key of 26?

Video: Number of Keys in Caesar Cipher (3 min; Feb 2020)

Exercise 6.2 (Caesar Cipher Decryption). You have received the ciphertext TBBQOLR. You know the Caesar cipher was used with key n. Find the plaintext.

Solution 6.2 (Caesar Cipher Decryption). To decrypt the ciphertext TBBQOLR with the key n, each letter in the ciphertext is decrypted by shifting n=13 positions to the left in the alphabet. The letter 13 positions to the left of T is g, as illustrated below:

A B C D E F g H I J K L M N O P Q R S T U V W X Y Z

The letter 13 positions to the left of B is o:

A B C D E F G H I J K L M N o P Q R S T U V W X Y Z

Therefore, the first three letters of the plaintext so far are goo. You can continue as above to find the final plaintext is goodbye.

Video: Caesar Cipher Decryption Example (3 min; Feb 2020)

We will now look at the Caesar cipher from a mathematical perspective. By treating each letter in the alphabet as a number, we can write equations that define the encrypt and decrypt operations on each letter.

Algorithm 6.2 (Caesar Cipher, formal).

C = E (K, P) = (P + K) mod 26

(6.1)

P = D (K, C) = (C - K) mod 26

(6.2)

In the equations, $P$ is the numerical value of a plaintext letter. Letters are numbered in alphabetical order starting at 0. That is, a=0, b=1, …, z=25. Similarly, $K$ and $C$ are the numerical values of the key and ciphertext letter, respectively. Shifting to the right in encryption is addition, while shifting to the left in decryption is subtraction. To cater for the wrap around (e.g. when the letter z is reacher), the last step is to mod by the total number of characters in the alphabet.

Exercise 6.3 (Caesar Cipher, formal). Consider the following mapping.

a b c d e f g h i j k l m

0 1 2 3 4 5 6 7 8 9 10 11 12

n o p q r s t u v w x y z

13 14 15 16 17 18 19 20 21 22 23 24 25

Use the the formal (mathematical) algorithm for Caesar cipher to decrypt SDV with key p.

Solution 6.3 (Caesar Cipher Encryption). Key p means $K$ = 15. The first ciphertext letter is S, so $C_{1}$ = 18. Using the decrypt equation:

\begin{array}{rcl} P_{1} & = & (C_{1} - K) mod 26 \\ = & (18 - 15) mod 26 \\ = & 3 mod 26 \\ = & 3 \end{array}

Therefore the first plaintext letter is d.

The same decrypt equation and key are used for the second ciphertext letter of D, i.e. $C_{2}$ = 3.

\begin{array}{rcl} P_{2} & = & (C_{2} - K) mod 26 \\ = & (3 - 15) mod 26 \\ = & (- 12) mod 26 \\ = & 14 \end{array}

Therefore the second plaintext letter is o.

The same decrypt equation and key are used for the third ciphertext letter of V, i.e. $C_{3}$ = 21.

\begin{array}{rcl} P_{3} & = & (C_{3} - K) mod 26 \\ = & (21 - 15) mod 26 \\ = & (6) mod 26 \\ = & 6 \end{array}

Therefore the third plaintext letter is g, and the entire plaintext is dog.

Video: Caesar Cipher Decryption using Mathematical Approach (4 min; Feb 2020)

[Caesar Encrypt and Decrypt]
> pycipher.Caesar(3).encipher("hello")
'KHOOR'
> pycipher.Caesar(3).decipher("khoor")
'HELLO'

Note that the pycipher package needs to be installed and imported first (see Section 3.3.2).

6.1.2 Brute Force Attack on Caesar Cipher

Definition 6.1 (Brute Force Attack). Try all combinations (of keys) until the correct plaintext/key is found.

Exercise 6.4 (Caesar Brute Force). The ciphertext FRUURJVBCANNC was obtained using the Caesar cipher. Find the plaintext using a brute force attack.

Solution 6.4. As a naive approach, try all possible keys, and then check the plaintext values obtained. If one is recognisable, then most likely have found the correct plaintext. Without any knowledge of which key was used, one approach is to try the keys in order. For example, try key 1, and then key 2, then key 3. (In theory you could try key 0, but we know in the Caesar cipher that it does nothing).

[Caesar Brute Force]
for k in range(0,26):
  pycipher.Caesar(k).decipher("FRUURJVBCANNC")

The range function in Python produces values inclusive of the lower limit and exclusive of the upper limit. That is, from 0 to 25.

[Caesar Brute Force Results]
0: FRUURJVBCANNC  13: SEHHEWIOPNAAP
1: EQTTQIUABZMMB  14: RDGGDVHNOMZZO
2: DPSSPHTZAYLLA  15: QCFFCUGMNLYYN
3: CORROGSYZXKKZ  16: PBEEBTFLMKXXM
4: BNQQNFRXYWJJY  17: OADDASEKLJWWL
5: AMPPMEQWXVIIX  18: NZCCZRDJKIVVK
6: ZLOOLDPVWUHHW  19: MYBBYQCIJHUUJ
7: YKNNKCOUVTGGV  20: LXAAXPBHIGTTI
8: XJMMJBNTUSFFU  21: KWZZWOAGHFSSH
9: WILLIAMSTREET  22: JVYYVNZFGERRG
10: VHKKHZLRSQDDS 23: IUXXUMYEFDQQF
11: UGJJGYKQRPCCR 24: HTWWTLXDECPPE
12: TFIIFXJPQOBBQ 25: GSVVSKWCDBOOD

The results of the brute force are formatted to show the key (it is slightly different from the Python code output).

Video: Brute Force Attack on Caesar Cipher with Python (5 min; Feb 2020)

Question 6.2 (How many attempts for Caesar brute force?). What is the worst, best and average case of number of attempts to brute force ciphertext obtained using the Caesar cipher?

There are 26 letters in the English alphabet. The key can therefore be one of 26 values, 0 through to 25. The key of 26 is equivalent to a key of 0, since it will encrypt to the same ciphertext. The same applies for all values greater than 25. While a key of 0 is not very smart, let’s assume it is a valid key.

The best case for the attacker is that the first key they try is the correct key (i.e. 1 attempt). The worst case is the attacker must try all the wrong keys until they finally try the correct key (i.e. 26 attempts). Assuming the encrypter chose the key randomly, there is equal probability that the attacker will find the correct key in 1 attempt (1/26), as in 2 attempts (1/26), as in 3 attempts (1/26), and as in 26 attempts (1/26). The average number of attempts can be calculated as (26+1)/2 = 13.5.

Assumption 6.1 (Recognisable Plaintext upon Decryption). The decrypter will be able to recognise that the plaintext is correct (and therefore the key is correct). Decrypting ciphertext using the incorrect key will not produce the original plaintext. The decrypter will be able to recognise that the key is wrong, i.e. the decryption will produce unrecognisable output.

Question 6.3 (Is plaintext always recognisable?). Caesar cipher is using recognisably correct plaintext, i.e. English words. But is the correct plaintext always recognisable? What if the plaintext was a different language? Or compressed? Or it was an image or video? Or binary file, e.g. .exe? Or a set of characters chosen randomly, e.g. a key or password?

The correct plaintext is recognisable if it contains some structure. That is, it does not appear random. It is common in practice to add structure to the plaintext, making it relatively easy to recognise the correct plaintext. For example, network packets have headers/trailers or error detecting codes. Later we will see cryptographic mechanisms that can be used to ensure that the correct plaintext will be recognised. For now, let’s assume it can be.

There are two ways to improve the Caesar cipher:

Increase the key space so brute force is harder
Change the plaintext (e.g. compress it) so harder to recognise structure

6.2 Monoalphabetic Ciphers

6.2.1 Monoalphabetic Cipher Definitions and Examples

Definition 6.2 (Permutation). A permutation of a finite set of elements is an ordered sequence of all the elements of $S$ , with each element appearing exactly once. In general, there are $n!$ permutations of a set with $n$ elements.

The concept of permutation is used throughput cryptography, and shortly we will see in a monoalphabetic (substitution) cipher.

Example 6.1 (Permutation). Consider the set $S = {a, b, c}$ . There are six permutations of $S$ :

abc, acb, bac, bca, cab, cba

This set has 3 elements. There are $3! = 3 \times 2 \times 1 = 6$ permutations.

Definition 6.3 (Monoalphabetic (Substitution) Cipher). Given the set of possible plaintext letters (e.g. English alphabetc, a–z), a single permutation is chosen and used to determine the corresponding ciphertext letter.

This is a monoalphabetic cipher because only a single cipher alphabet is used per message.

Example 6.2 (Monoalphabetic (Substitution) Cipher). In advance, the sender and receiver agree upon a permutation to use, e.g.:
P: a b c d e f g h i j k l m n o p q r s t u v w x y z
C: H P W N S K L E V A Y C X O F G T B Q R U I D J Z M
To encrypt the plaintext hello, the agreed upon permutation (or mapping) is used to produce the ciphertext ESCCF.

Exercise 6.5 (Decrypt Monoalphabetic Cipher). Decrypt the ciphertext QSWBSR using the permutation chosen in the previous example.

Solution 6.5 (Decrypt Monoalphabetic Cipher). A simple lookup on the mapping defined in the example returns the plaintext secret.

Video: Mono-alphabetic Substitution Cipher Example (3 min; Feb 2020)

Question 6.4 (How many keys in English monoalphabetic cipher?). How many possible keys are there for a monoalphabetic cipher that uses the English lowercase letters? What is the length of an actual key?

Consider the number of permutations possible. The example used a single permutation chosen by the two parties.

Video: Number of Keys in an English Monoalphabetic Substitution Cipher (3 min; Feb 2020)

6.2.2 Brute Force Attack on Monoalphabetic Cipher

Exercise 6.6 (Brute Force on Monoalphabetic Cipher). You have intercepted a ciphertext message that was obtained with an English monoalphabetic cipher. You have a Python function called:
mono_decrypt_and_check(ciphertext,key)
that decrypts the ciphertext with a key, and returns the plaintext if it is correct, otherwise returns false. You have tested the Python function in a while loop and the computer can apply the function at a rate of 1,000,000,000 times per second. Find the average time to perform a brute force on the ciphertext.

Solution 6.6 (Brute Force on Monoalphabetic Cipher). With a 26 letter alphabet, there are $26!$ permutations or keys. The average number of keys to try in a brute force attack is $(26! + 1) ∕ 2$ , or approximately half of them, $26! ∕ 2$ . The Python code can try $1 0^{9}$ keys per second. Therefore the average brute force time, $T$ , is:

\begin{array}{rcl} T & = & \frac{(26! + 1) ∕ 2}{1 0^{9}} \\ \approx & \frac{2 \times 1 0^{26}}{1 0^{9}} \\ \approx & 2 \times 1 0^{17} seconds \\ \approx & 64 million centuries \end{array}

Video: Brute Force Attack Time on English Monoalphabetic Cipher (7 min; Feb 2020)

6.2.3 Frequency Analysis Attack on Monoalphabetic Cipher

Brute force is the “dumb” approach to breaking a cipher. While it was sufficient in breaking the Caesar cipher, it is not feasible for a monoalphabetic substitution cipher. Can we take a “smart” approach that would take less effort than brute force? Often we can. Let’s consider frequency analysis as an alternative to a brute force attack.

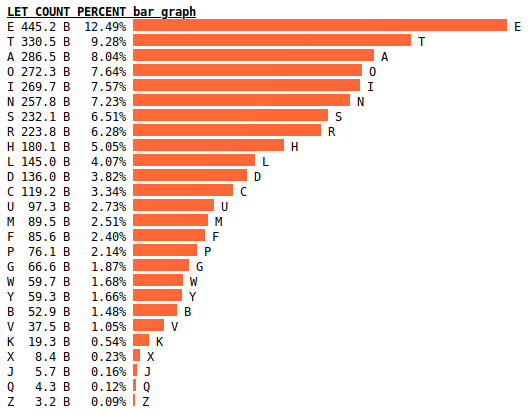
Definition 6.4 (Frequency Analysis Attack). Find (portions of the) key and/or plaintext by using insights gained from comparing the actual frequency of letters in the ciphertext with the expected frequency of letters in the plaintext. Can be expanded to analyse sets of letters, e.g. digrams, trigrams, n-grams, words.

Credit: Letter Counts by Peter Norvig

Figure 6.1: Relative Frequency of Letters by Norvig

The letter frequencies of the figure above are based on Peter Norvig’s analysis of Google Books N-Gram Dataset. Norvig is Director of Research at Google. His website has more details on the analysis.

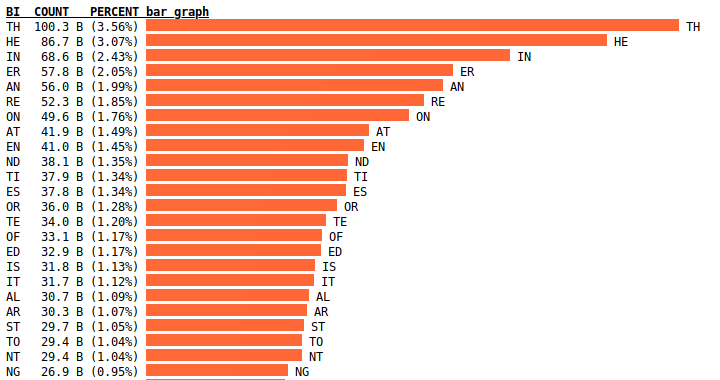
Credit: Two-Letter Sequence (Bigram) Counts by Peter Norvig

Figure 6.2: Relative Frequency of Digrams by Norvig

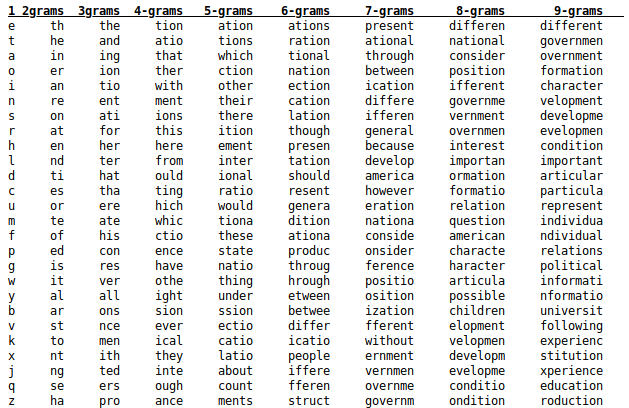
Credit: N-Letter Sequences (N-grams)" by Peter Norvig

Figure 6.3: Relative Frequency of N-Grams by Norvig

Exercise 6.7 (Break a Monoalphabetic Cipher). Ciphertext:

ziolegxkltqodlzgofzkgrxetngxzgzithkofeohs

tlqfrzteifojxtlgyltexkofuegdhxztklqfregd

hxztkftzvgkalvoziygexlgfofztkftzltexkoznz

itegxkltoltyytezoctsnlhsozofzgzvghqkzlyo

klzofzkgrxeofuzitzitgkngyeknhzgukqhinofes

xrofuigvdqfnesqlloeqsqfrhghxsqkqsugkozid

lvgkaturtlklqrouozqsloufqzxktlqfrltegfrhk

gcorofurtzqoslgyktqsofztkftzltexkoznhkgz

gegslqsugkozidlqfrziktqzltuohltecokxltlyo

ktvqsslitfetngxvossstqkfwgzizitgktzoeqsq

lhtezlgyegdhxztkqfrftzvgkaltexkoznqlvtssq

ligvziqzzitgknolqhhsotrofzitofztkftzziol

afgvstrutvossitshngxofrtloufofuqfrrtctsgh

ofultexktqhhsoeqzogflqfrftzvgkahkgzgegsl

qlvtssqlwxosrofultexktftzvgkal

Solution 6.7 (Break a Monoalphabetic Cipher). See the the steps under the section “Frequency Analysis of Monoalphabetic Cipher” on the following website:

sandilands.info/sgordon/classical-ciphers-frequency-analysis-examples

6.3 Playfair Cipher

Algorithm 6.3 (Playfair Matrix Construction). Write the letters of keyword k row-by-row in a 5-by-5 matrix. Do not include duplicate letters. Fill the remainder of the matrix with the alphabet. Treat the letters i and j as the same (that is, they are combined in the same cell of the matrix).

Exercise 6.8 (Playfair Matrix Construction). Construct the Playfair matrix using keyword australia.

Solution 6.8 (Playfair Matrix Construction). We write the keyword in a 5-by-5 matrix, starting as:

a u s t r

l i

Note that we don’t write the letter a multiple times in the matrix, and the letter i also represents the letter j.

Now we fill the remainder of the matrix with the English letters in alphabetical order. Again, no duplicate letters are included.

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

Video: Playfair Cipher Matrix Construction (3 min; Feb 2020)

Algorithm 6.4 (Playfair Encryption). Split the plaintext into pairs of letters. If a pair has identical letters, then insert a special letter x in between. If the resulting set of letters is odd, then pad with a special letter x.

Locate the plaintext pair in the Playfair matrix. If the pair is on the same column, then shift each letter down one cell to obtain the resulting ciphertext pair. Wrap when necessary. If the plaintext pair is on the same row, then shift to the right one cell. Otherwise, the first ciphertext letter is that on the same row as the first plaintext letter and same column as the second plaintext letter, and the second ciphertext letter is that on the same row as the second plaintext letter and same column as the first plaintext letter.

Repeat for all plaintext pairs.

Playfair decryption uses the same matrix and reverses the rules. That is, move up (instead of down) if on the same column, move left (instead of right) if on the same row. Finally, the padded special letters need to be removed. This can be done based upon knowledge of the langauge. For example, if the intermediate plaintext from decryption is helxlo, then as that word doesn’t exist, the x is removed to produce hello.

Exercise 6.9 (Playfair Encryption). Find the ciphertext if the Playfair cipher is used with keyword australia and plaintext hello.

Solution 6.9 (Playfair Encryption). The Playfair matrix from the previous exercise is:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

First split the plaintext into pairs: he, ll and o. As the second pair has identical letters, insert a special character x and move the second l into the third pair. The resulting pairs are:

he lx lo

Now for each pair, apply the rules to find the corresponding ciphertext pair.

For plaintext pair he:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

As the pair are on the same row, the ciphertext pair is taken as the letters to the right:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

The first two letters of the ciphertext are KF.

The second pair, lx, is on different rows and columns:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

The ciphertext pair is taken from the same row and column, but reversed in order:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

The second pair of ciphertext is BV.

Finally, the third pair:

a u s t r

l i b c d

e f g h k

m n o p q

v w x y z

As a result, the final ciphertext is KFBVBM.

Video: Encryption with the Playfair Cipher (7 min; Feb 2020)

Question 6.5 (Does Playfair cipher always map a letter to the same ciphertext letter?). Using the Playfair cipher with keyword australia, encrypt the plaintext hellolove.

With the Playfair cipher, if a letter occurs multiple times in the plaintext, will that letter always encrypt to the same ciphertext letter?

If a pair of letters occurs multiple times, will that pair always encrypt to the same ciphertext pair?

Is the Playfair cipher subject to frequency analysis attacks?

Video: Playfair Cipher and Frequency Analysis (4 min; Feb 2020)

6.4 Polyalphabetic Ciphers

Definition 6.5 (Polyalphabetic (Substitution) Cipher). Use a different monoalphabetic substitution as proceeding through the plaintext. A key determines which monoalphabetic substitution is used for each transformation.

For example, when encrypting a set of plaintext letters with a polyalphabetic cipher, a monoalpabetic cipher with a particular key is used to encrypt the first letter, and then the same monoalphabetic cipher is used but with a different key to encrypt the second letter. They key used for the monoalphabetic cipher is determined by the key (or keyword) for the polyalphabetic cipher.

Vigenère Cipher: uses Caesar cipher, but Caesar key changes each letter based on keyword
Vernam Cipher: binary version of Vigenère, using XOR
One Time Pad: same as Vigenère/Vernam, but random key as long as plaintext

Selected polyalphabetic ciphers are explained in depth in the following sections.

6.5 Vigenère Cipher

Algorithm 6.5 (Vigenère Cipher). For each letter of plaintext, a Caesar cipher is used. The key for the Caesar cipher is taken from the Vigenère key(word), progressing for each letter and wrapping back to the first letter when necessary. Formally, encryption using a keyword of length $m$ is:

c_{i} = (p_{i} + k_{i mod m}) mod 26

where $p_{i}$ is letter $i$ (starting at 0) of plaintext $P$ , and so on.

Simply, Vigenère cipher is just the Caesar cipher, but changing the Caesar key for each letter encrypted/decrypted. The Caesar key is taken from the Vigenère key. The Vigenère key is not a single value/letter, but a set of values/letters, and hence referred to as a keyword. Encrypting the first letter of plaintext uses the first key from the keyword. Encrypting the second letter of plaintext uses the second key from the keyword. And so on. As the keyword (for convenience) is usually shorter than the plaintext, once the end of the keyword is reached, we return to the first letter, i.e. wrap around.

In the formal equation for encryption, $i$ represents letter $i$ (starting at 0) of the plaintext. For example, if the keyword is 6 letters, when encrypting letter 8 of the plaintext (that is the 9th), then $k_{2}$ is used, i.e. the 3rd letter from the keyword.

Example 6.3 (Vigenère Cipher Encryption). Using the Vigenère cipher to encrypt the plaintext carparkbehindsupermarket with the keyword sydney produces the ciphertext UYUCEPCZHUMLVQXCIPEYUXIR. The keyword would be repeated when Caesar is applied:
P: carparkbehindsupermarket
K: sydneysydneysydneysydney
C: UYUCEPCZHUMLVQXCIPEYUXIR

Note that the first a in the plaintext transforms to Y, while the second a transforms to E. With polyalphabetic ciphers, the same plaintext letters do not necessarily always transform to the same ciphertext letters. Although they may: look at the third a.

Video: Encryption with Vigenere Cipher and Python (4 min; Feb 2020)

Exercise 6.10 (Vigenère Cipher Encryption). Use Python (or other software tools) to encrypt the plaintext centralqueensland with the following keys with the Vigenère cipher, and investigate any possible patterns in the ciphertext: cat, dog, a, giraffe.

Solution 6.10 (Vigenère Cipher Encryption). Using the pycipher library:

$ python3
Python 3.6.9 (default, Nov 7 2019, 10:44:02)
[GCC 8.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import pycipher
>>> pycipher.Vigenere("cat").encipher("centralqueensland")
’EEGVRTNQNGEGULTPD’
>>> pycipher.Vigenere("dog").encipher("centralqueensland")
’FSTWFGOEAHSTVZGQR’
>>> pycipher.Vigenere("a").encipher("centralqueensland")
’CENTRALQUEENSLAND’
>>> pycipher.Vigenere("giraffe").encipher("centralqueensland")
’IMETWFPWCVESXPGVU’

Video: Vigenere Python Examples (4 min; Feb 2020)

While the Vigenère cipher improves on monoalphabetic ciphers, it still has a weakness. The approach for breaking the cipher is:

Determine the length of the keyword m
- Repeated n-grams in the ciphertext may indicate repeated n-grams in the plaintext
- Separation between repeated n-grams indicates possible keyword length $m$
- If plaintext is long enough, multiple repetitions make it easier to find $m$
Treat the ciphertext as that from m different monoalphabetic ciphers
- E.g. Caesar cipher with $m$ different keys
- Break the monoalphabetic ciphers with frequency analysis
With long plaintext, and repeating keyword, Vigenère can be broken

The following shows an example of breaking the Vigenère cipher, although it is not necessary to be able to do this yourself manually.

Example 6.4 (Breaking Vigenère Cipher). Ciphertext ZICVTWQNGRZGVTWAVZHCQYGLMGJ has repetition of VTW. That suggests repetition in the plaintext at the same position, which would be true if the keyword repeated at the same position.
012345678901234567890123456
ZICVTWQNGRZGVTWAVZHCQYGLMGJ
That is, it is possible the key letter at position 3 is the repated at position 12. That in turn suggest a keyword length of 9 or 3.
ciphertext ZICVTWQNGRZGVTWAVZHCQYGLMGJ
length=3: 012012012012012012012012012
length=9: 012345678012345678012345678
An attacker would try both keyword lengths. With a keyword length of 9, the attacker then performs Caesar cipher frequency analysis on every 9th letter. Eventually they find plaintext is wearediscoveredsaveyourself and keyword is deceptive.

This attack may require some trial-and-error, and will be more likely to be successful when the plaintext is very long. See the Stallings textbook, from which the example is taken, for further explanation.

Video: Cryptanalysis of Vigenere Cipher (4 min; Feb 2020)

6.6 Vernam Cipher

Before looking at an improvement of the Vigenère cipher, let’s look at a cipher that is essentially the same but operates on binary data.

Algorithm 6.6 (Vernam Cipher). Encryption is performed as:

c_{i} = p_{i} \oplus k_{i}

decryption is performed as:

p_{i} = c_{i} \oplus k_{i}

where $p_{i}$ is the $i$ th bit of plaintext, and so on. The key is repeated where necessary.

The Vernam cipher is essentially a binary form of the Vigenère cipher. The mathematical form of Vigenère encryption adds the plaintext and key and mods by 26 (where there are 26 possible charactersd). In binary, there are 2 possible characters, so the equivalnet is to add the plaintext and key and mod by 2. This identical to the XOR operation.

To demonstrate the Vernam cipher, we will use Python to perform the XOR ( $\oplus$ ) operation.

[XOR]
> def xor(x, y):
...     return '{1:0{0}b}'.format(len(x), int(x, 2) ^ int(y, 2))
...

The Python code defines a function called xor that takes two strings representing bits, and returns a string represent the XOR of those bits. The actual XOR is performed on integers using the Python hat ôperator. The rest is formatting as strings.

Exercise 6.11 (Vernam Cipher Encryption). Using the Vernam cipher, encrypt the plaintext 011101010101000011011001 with the key 01011.

[Vernam Cipher Encryption]
> xor('011101010101000011011001','010110101101011010110101')
'001011111000011001101100'

Video: Vernam Cipher using Bits and XOR (7 min; Feb 2020)

6.7 One Time Pad

The weakness of the Vigenère and Vernam ciphers is a repeating keyword. The solution is to use a key as long as the plaintext and entirely random.

Algorithm 6.7 (One-Time Pad). Use polyalphabetic cipher (such as Vigenère or Vernam) but where the key must be: random, the same length as the plaintext, and not used multiple times.

Essentially, the Vigenère or Vernam become a One-Time Pad (OTP) if the keys are chosen appropriately.

The result of using a long, random key is the OTP has the following properties:

Encrypting plaintext with random key means output ciphertext will be random
- E.g. XOR plaintext with a random key produces random sequence of bits in ciphertext
Random ciphertext contains no information about the structure of plaintext
- Attacker cannot analyse ciphertext to determine plaintext
Brute force attack on key is ineffective
- Multiple different keys will produce recognisable plaintext
- Attacker has no way to determine which of the plaintexts are correct
OTP is only known unbreakable (unconditionally secure) cipher

Example 6.5 (Attacking OTP). Consider a variant of Vigenère cipher that has 27 characters (including a space). An attacker has obtained the ciphertext:
ANKYODKYUREPFJBYOJDSPLREYIUNOFDOIUERFPLUYTS

Attacker tries all possible keys. Two examples:
k1: pxlmvmsydofuyrvzwc tnlebnecvgdupahfzzlmnyih
p1: mr mustard with the candlestick in the hall
k2: pftgpmiydgaxgoufhklllmhsqdqogtewbqfgyovuhwt
p2: miss scarlet with the knife in the library

There are many other legible plaintexts obtained with other keys. No way for attacker to know the correct plaintext

The example shows that even a brute force attack on a OTP is unsuccessful. Even if the attacker could try all possible keys—the plaintext is 43 characters long and so there are $2 7^{43} \approx 1 0^{61}$ keys—they would find many possible plaintext values that make sense. The example shows two such plaintext values that the attacker obtained. Which one is the correct plaintext? They both make sense (in English). The attacker has no way of knowing. In general, there will be many plaintext values that make sense from a brute force attack, and the attacker has no way of knowing which is the correct (original) plaintext. Therefore a brute force attack on a OTP is ineffective.

Let’s finish our coverage of classical substitition ciphers with a summary of the OTP:

Only known unbreakable (unconditionally secure) cipher
- Ciphertext has no statistical relationship with plaintext
- Given two potential plaintext messages, attacker cannot identify the correct message
But two significant practical limitations:
1. Difficult to create large number of random keys
2. Distributing unique long random keys is difficult
Limited practical use

The practical limittions are significant. The requirement that the key must be as long as the plaintext, random and never repeated (if it is repeated then the same problems arise as in the original Vernam cipher) means large random values must be created. But creating a large amount of random data is actually difficult. Imagine you wanted to use a OTP for encrypting large data transfers (multiple gigabytes) across a network. Multiple gigabytes of random data must be generated for the key, which is time consuming (seconds to hours) for some computers. Also, the key must be exchanging, usually over a network, with the other party in advance. So to encrypt a 1GB file to need a 1GB random key. Both the key and file must be sent across the network, i.e. a total of 2GB. This is very inefficient use of the network: a maximum of 50% efficiency.

Later we will see real ciphers that work with a relatively small, fixed length key (e.g. 128 bits) and provide sufficient security.

Video: One-Time Pad as an Unbreakable Cipher (7 min; Feb 2020)

6.8 Transposition Techniques

The previous set of classical ciphers use a substitution operation, replacing one character with another from the character set. A different approach is to simply re-arrange the set of characters within the plaintext. These type of ciphers are called transposition or permutation techniques.

Substitution: replace one (or more) character in plaintext with another from the entire possible character set
Transposition: re-arrange the characters in the plaintext
- The set of characters in the ciphertext is the same as in the plaintext
- Problem: the plaintext frequency statistics are also in the ciphertext
On their own, transposition techniques are easy to break
Combining transposition with substitution makes ciphers stronger, and building block of modern ciphers

Definition 6.6 (Rail Fence Cipher Encryption). Select a depth as a key. Write the plaintext in diagonals in a zig-zag manner to the selected depth. Read row-by-row to obtain the ciphertext.

The decryption process can easily be derived from the encryption algorithm.

Exercise 6.12 (Rail Fence Encryption). Consider the plaintext securityandcryptography with key 4. Using the rail fence cipher, find the ciphertext.

Solution 6.11 (Rail Fence Encryption). With a key of 4, we write the plaintext in diagonals over 4 rows.
s t r r
e i y c y g a
c r a d p o p y
u n t h

The ciphertext is obtained by reading row-by-row: STRREIYEYGACRADPOPYUNTH.

Video: Rail Fence Transposition Cipher Example (2 min; Feb 2020)

Definition 6.7 (Rows Columns Cipher Encryption). Select a number of columns $m$ and permutate the integers from 1 to $m$ to be the key. Write the plaintext row-by-row over $m$ columns. Read column-by-column, in order of the columns determined by the key, to obtain the ciphertext.

Be careful with the decryption process; it is often confusing. Of course it must be the process such that the original plaintext is produced.

Exercise 6.13 (Rows Columns Encryption). Consider the plaintext securityandcryptography with key 315624. Using the rows columns cipher, find the ciphertext.

Solution 6.12 (Rows Columns Encryption). With a key of 315624, we write the plaintext row-by-row across 6 columns:

3 1 5 6 2 4
s e c u r i
t y a n d c
r y p t o g
r a p h y x

A special letter, x in this case, is used to pad to fill the last row. This padding must be agreed upon in advance by the sender and receiver.

Now read column-by-column, starting with column indicated by the key as 1, i.e. EYYA. Then column 2: RDOY. The resulting ciphertext is EYYARDOYSTRRICGXCAPPUNTH.

Video: Encrypting with Rows/Columns Transposition Cipher (3 min; Feb 2020)

Example 6.6 (Rows Columns Multiple Encryption). Assume the ciphertext from the previous example has been encrypted again with the same key. The resulting ciphertext is YYCPRRCTEOIPDRAHYSGUATXH. Now let’s view how the cipher has “mixed up” the letters of the plaintext. If the plaintext letters are numbered by position from 01 to 24, their order (split across two rows) is:
01 02 03 04 05 06 07 08 09 10 11 12
13 14 15 16 17 18 19 20 21 22 23 24

After first encryption the order becomes:
02 08 14 20 05 11 17 23 01 07 13 19
06 12 18 24 03 09 15 21 04 10 16 22

After the second encryption the order comes:
08 23 12 21 05 13 03 16 02 17 06 15
11 19 09 20 14 01 18 04 20 07 24 10
Are there any obviously obversvable patterns?

After the first encryption, the numbers reveal a pattern: increasing by 6 within groups of 4. This is because of the 6 columns and 4 rows. After the second encryption, it is not so obvious to identify patterns.

The point is that while a single application of the transposition cipher did not seem to offer much security (in terms of hiding patterns), adding the second application of the cipher offers an improvement. This principle of repeated applications of simple operations is used in modern ciphers.

In summary:

Transposition ciphers on their own offer no practical security
But combining transposition ciphers with substitution ciphers, and repeated applications, practical security can be achieved
Modern symmetric ciphers use multiple applications (rounds) of substitition and transposition (permutation) operations

Video: Multiple Rounds of Rows/Columns Transposition Cipher (5 min; Feb 2020)

[next] [front] [up]

Chapter 6Classical Ciphers

6.1 Caesar Cipher

6.1.1 Caesar Cipher Definitions and Examples

6.1.2 Brute Force Attack on Caesar Cipher

6.2 Monoalphabetic Ciphers

6.2.1 Monoalphabetic Cipher Definitions and Examples

6.2.2 Brute Force Attack on Monoalphabetic Cipher

6.2.3 Frequency Analysis Attack on Monoalphabetic Cipher

6.3 Playfair Cipher

6.4 Polyalphabetic Ciphers

6.5 Vigenère Cipher

6.6 Vernam Cipher

6.7 One Time Pad

6.8 Transposition Techniques

Chapter 6
Classical Ciphers