Chapter 9
Advanced Encryption Standard

File: crypto/aes.tex, r1980

This chapter provides details of Advanced Encryption Standard (AES), with concepts demonstrated via a simplified, educational version called Simplified Advanced Encryption Standard (S-AES). Many of the details serve mainly as reference, with little discussion.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

9.1 Overview of AES

As the 56-bit key of DES became a practical limitation, researchers and standard bodies worked towards new block ciphers.

• 1977: DES (56-bit key). NIST published.
• 1991: IDEA, similar to DES, secure but patent issues
• 1999: 3DES (168-bit key). NIST recommended 3DES be used (DES only for legacy systems)
  • 3DES was considered secure (apart from special case attacks)
  • But 3DES is very slow, especially in software
  • DES and 3DES use 64-bit blocks – larger block sizes required for efficiency
• 1997: NIST called for proposals for new Advanced Encryption Standards
  • Proposals made public and evaluations performed
• 2001: Selected Rijndael as the algorithm for AES

The process for determining the algorithm to be selected for AES was performed as a multi-round competition run by NIST. There are varying criteria for selecting a winner.

• Original NIST criteria:
  • Security: effort to cryptoanalyse algorithm, randomness, …
  • Cost: royalty-free license, computationally efficient, …
  • Algorithm and implementation characteristics: flexibility (different keys/blocks, implement on different systems), simplicity, …
• 21 candidate algorithms reduced to 5
• Updated NIST evaluation criteria for 5 algorithms:
  • General Security
  • Software and hardware implementations (needs to be efficient)
  • Low RAM/ROM requirements (e.g. for smart cards)
  • Ability to change keys quickly
  • Potential to use parallel processors

Rijndael, a proposal by Vincent Rijmen and Joan Daemen, was selected the winner for the following reasons:

• Security: good, no known attacks
• Software implementation: fast, can make use of parallel processors
• Hardware implementation: fastest of all candidates
• Low memory requirements: good, except encryption and decryption require separate space
• Timing and Power analysis attacks: easiest to defend against
• Key flexibility: supports on-the-fly change of keys and different size of keys/blocks

Key parameters of Rijndael were the block and key sizes. While the Rijndael support various sizes, the eventual NIST standard settling on a single block size with three key lengths.

• NIST Advanced Encryption Standard, FIPS-197, 2001
• Three variations of same algorithm standardised
  • AES-128: 128-bit key, 10 rounds
  • AES-192: 192-bit key, 12 rounds
  • AES-256: 256-bit key, 14 rounds
• AES uses 128-bit block size for all variations
• Simplified Advanced Encryption Standard (S-AES) used to understand AES (educational only)
• For details of AES see the Stallings textbook, AES on Wikipedia or the AES standard from NIST

9.2 Simplified-AES

• Educational purposes only. Mohammad A. Musa , Edward F. Schaefer and Stephen Wedig (2003) A Simplified AES Algorithm and its Linear and Differential Cryptanalyses, Cryptologia, 27:2, 148-177, DOI: 10.1080/0161-110391891838
• Input: 16-bit block of plaintext; 16-bit key
• Output: 16-bit block of ciphertext
• Operations:
  • Add Key: XOR of a 16-bit key and 16-bit state matrix
  • Nibble Substitution: S-Box table lookup that swaps nibbles (4 bits)
  • Shift Row: shift of nibbles in a row
  • Mix Column: re-order columns
  • Rotate Nibbles: swap the nibbles
• 3 rounds (although they don’t contain same operations)

S-AES operates on 16-bit blocks, with some operations on 8-bit words and others on 4-bit nibbles. For example, a 16-bit block is equivalent to two 8-bit words or four 4-bit nibbles.

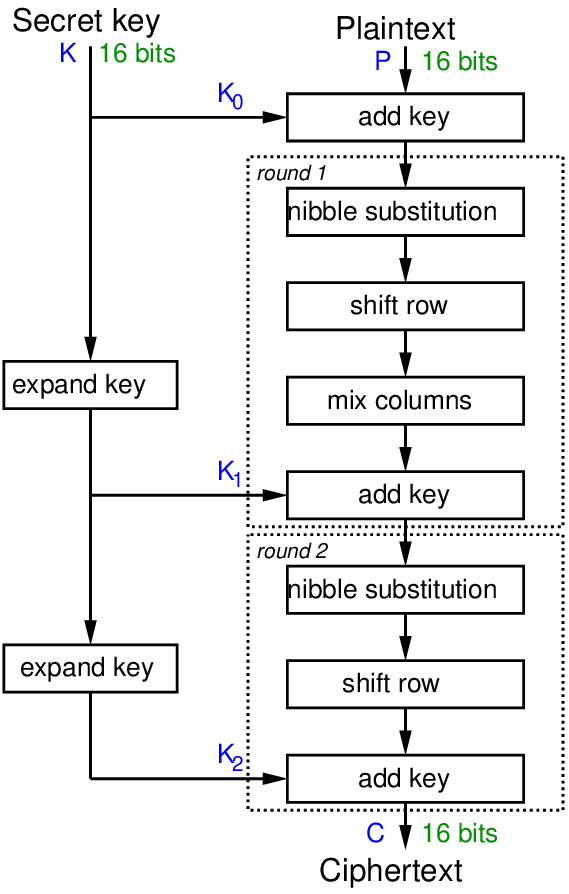
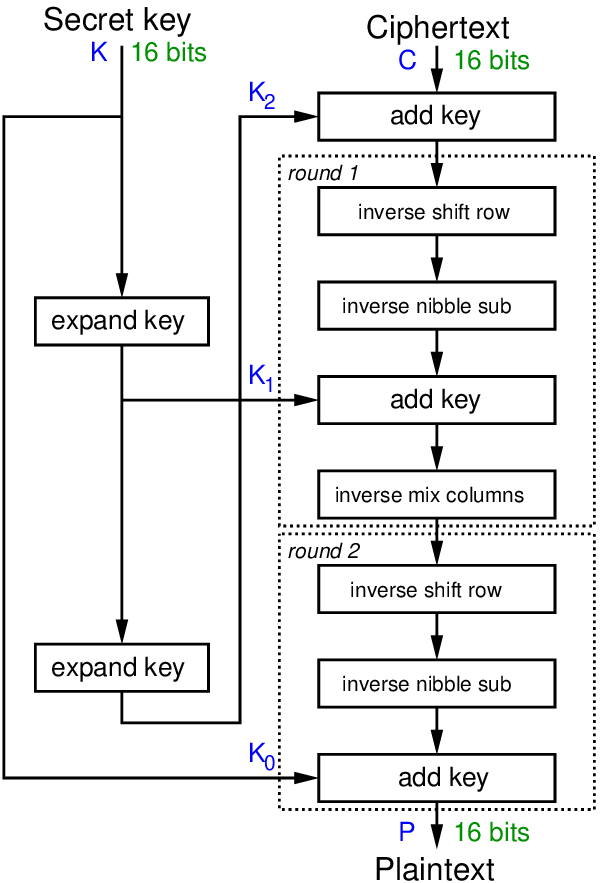
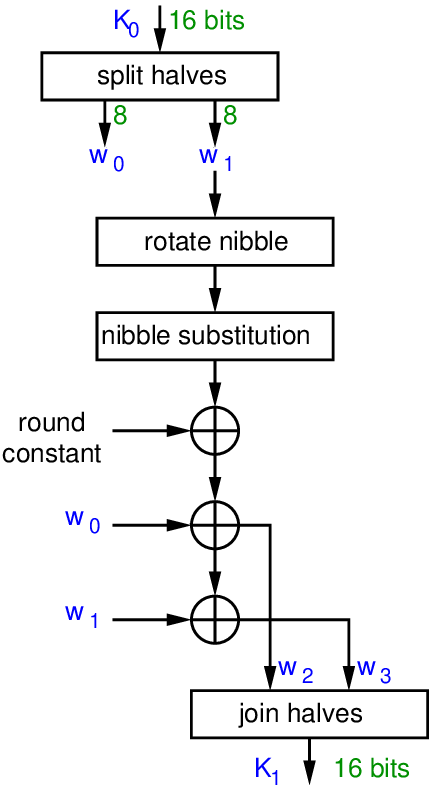
Figure 9.1, Figure 9.2, and Figure 9.3 show the encryption, decryption and key generation algorithms, respectively. The operations used in the algorithms are defined later.

Figure 9.1 shows the overall steps for S-AES and key expansion and encryption. The key generation takes a 16-bit secret key and expands that into 3 16-bit round keys. The first round key $K_0$ is simple the original key. The next two round keys, $K_1$ and $K_2$ are generated by an expansion algorithm. Figure 9.3 shows that algorithm for $K_1$.

S-AES encryption operates on 16-bit blocks of plaintext. To encrypt, there is an initial add key, and then two rounds, where the 2nd round does not include the mix columns operation.

Figure 9.2 shows the decryption operations. Note that it is similar to encryption in reverse, with all operations replaced with their inverse operations. The same round keys are used as in encryption, but in the opposite order.

Figure 9.3 shows the key generation operations for generated round key $K_1$. Similar steps are used to generate $K_2$, where the input is $K_1$ and a different round constant.

While S-AES operates on 16-bits at a time, those bits are viewed as a state matrix of 4 nibbles. Note the matrix is filled columnwise, with the first 8 bits (2 nibbles) in the first column.

The following shows operations based on the state matrix.

Shift Row swaps the 2nd nibble with the 4th nibble. Add Key is a bitwise XOR. The round constants are used in the key generation.

The left-most 2 bits in a nibble determine the row, and the right-most 2 bits in the nibble determine the column. The output nibble is based on the S-Box. The Inverse S-Box is used in decryption.

$S^{\prime }$ denotes the output from the mixing of columns, e.g. $S_{0,0}^{\prime }=\left(1\times S_{0,0}\right)+\left(4\times S_{1,0}\right)$. Importantly, the resulting addition and multiplication operations are in Galois Field GF($2^4$). We do not cover (Galois) fields, however in Number Theory we saw modular arithmetic with mod $n$ where all operations produced results within 0 to $n$. This is a simple case of a field, i.e. all operations produce answers within some finite range. GF($2^4$) means all answers will be within range 0 to 15.

GF($2^4$) addition is equivalent to bitwise XOR. However GF($2^4$) multiplication is more complicated. Therefore, for the purpose of demonstrating S-AES, a simplified view of the mix column operations with a table lookup for multiplication is shown in the following.

Figure 9.4 shows the GF($2^4$) multiplication table in binary. The green column is used in encryption (Mix Columns) and the two blue columns are used in decryption (Inverse Mix Columns). For example with encryption, when multiplying a value by 4 (0100 in binary), lookup the value in the first column (e.g. 0111) and the answer will be in the green column (e.g. 1111).

Now let’s compare S-AES to the real AES, specifically AES-128.

• S-AES
  • 16-bit key, 16-bit plaintext/ciphertext
  • 2 rounds: first with all 4 operations, last with 3 operations
  • Round key size: 16 bits
  • Mix Columns: arithmetic over GF($2^4$)
• AES-128
  • 128-bit key, 128-bit plaintext/ciphertext
  • 10 rounds: first 9 with all 4 operations, last with 3 operations
  • Round key size: 128 bits
  • Mix Columns: arithmetic over GF($2^8$)
• Principles of operation are the same

9.3 Simplified-AES Example

9.4 AES in OpenSSL

9.4.1 AES Encryption Basics in OpenSSL

You can use AES in a similar manner to DES in OpenSSL (see Section 8.4), that is, using the enc operation. The following is an example of AES encryption with a 128 bit key and CTR mode of operation. In addition to the key, an IV is needed. The plaintext2.in file is just an example, in fact it is obtained from copying the actual OpenSSL binary, e.g. cp /usr/bin/openssl plaintext2.in.

$ openssl enc -aes-128-ctr -in plaintext2.in -out ciphertext2.bin -K 0123456789abcdef0123456789abcdef -iv 00000000000000000000000000000000
$ openssl enc -d -aes-128-ctr -in ciphertext2.bin -out plaintext2.out -K 0123456789abcdef0123456789abcdef -iv 00000000000000000000000000000000
$ ls -l *2*
-rw-rw-r-- 1 sgordon sgordon 513208 Jul 31 14:29 ciphertext2.bin
-rwxr-xr-x 1 sgordon sgordon 513208 Jul 31 13:32 plaintext2.in
-rw-rw-r-- 1 sgordon sgordon 513208 Jul 31 14:30 plaintext2.out
$ diff plaintext2.in plaintext2.out
$ xxd -l 96 ciphertext2.bin 
0000000: 06ee 8984 3a69 ac84 d388 ce61 110a 6274  ....:i.....a..bt
0000010: c1ed f9ed f193 f2d2 bf8d 29e2 1577 5d32  ..........)..w]2
0000020: 1e25 cc36 bb37 baa7 eb65 402b a8ef 421b  .%.6.7...e@+..B.
0000030: a6f7 073c a08a e698 747d 5153 8df1 ed88  ...<....t}QS....
0000040: 1131 f4e0 2014 1392 ee36 2b54 27eb ca72  .1.. ....6+T'..r
0000050: 4b88 e623 ed28 2da7 87cd 0c1a 5441 5d7c  K..#.(-.....TA]|

Both the Key (note uppercase -K) and IV were specified on the command line as a hexadecimal string. With AES-128, they must be 32 hex digits (128 bits). You may choose any value you wish.

Use the list operation in OpenSSL to see the variants of AES supported by OpenSSL (see Section 3.2.3).

9.4.2 AES Performance Benchmarking

OpenSSL has a built-in operation for performance testing. It encrypts random data over short period, measuring how many bytes can be encrypted per second. It can be used to compare the performance of different algorithms, and compare the performance of different computers.

To run performance tests across a large set of algorithms, simple use the speed operation. Note that it may take a few minutes:

$ openssl speed
...

You can select the algorithms to test, e.g. AES, DES and Message Digest 5 hash function (MD5):

$ openssl speed aes-128-cbc des md5
...
The 'numbers' are in 1000s of bytes per second processed.
type             16 bytes     64 bytes    256 bytes   1024 bytes   8192 bytes
md5              68101.86k   199387.83k   444829.62k   639419.85k   734323.76k
des cbc          76810.00k    78472.53k    78442.77k    79241.85k    78440.45k
des ede3         28883.98k    29585.17k    29640.69k    29499.08k    29740.52k
aes-128 cbc     138894.09k   150561.30k   154512.15k   155203.81k   155590.46k

The output shows the progress, the versions and options used for OpenSSL and then a summary table at the end. Focus on the summary table, and the last line (for aes-128-cbc) in the example above. The speed test encrypts as many b Byte input plaintexts as possible in a period of 3 seconds. Different size inputs are used, i.e. b = 16, 64, 256, 1024 and 8192 Bytes. The summary table reports the encryption speed in Bytes per second. So if 25955833 16-Byte plaintext values are encrypted in 3 seconds, then the speed reported in the summary table is $25955833\times 16÷3\approx 138$ million Bytes per second. You can see that value (138,894.09kB/s) in the table above. So AES using 128 bit key and CBC can encrypt about 138 MB/sec when small plaintext values are used and 155 MB/sec when plaintext values are 8192 Bytes.

Normally OpenSSL implements all algorithms in software. However recent Intel CPUs include instructions specifically for AES encryption, a feature referred to as AES-NI. If an application such as OpenSSL uses this special instruction, then part of the AES encryption is performed directly by the CPU. This is usually must faster (compared to using general instructions). To run a speed test that uses the Intel AES-NI, use the evp option:

$ openssl speed -evp aes-128-cbc
...
type             16 bytes     64 bytes    256 bytes   1024 bytes   8192 bytes
aes-128-cbc     689927.75k   729841.81k   745383.38k   747226.84k   747784.87k

Compare the values to the original results. In the original test we achieved 138 MB/sec. Using the Intel AES hardware encryption we get a speed of 689 MB/sec, about 5 times faster.

9.4.3 AES OpenSSL Exercises

9.5 AES in Python

The Python Cryptography library includes symmetric key encryption using various algorithms, including AES. See the examples for generic symmetric encryption at:

• https://cryptography.io/en/latest/hazmat/primitives/symmetric-encryption/