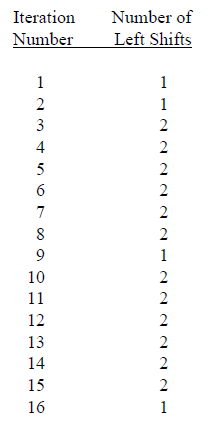Chapter 8
Data Encryption Standard

File: crypto/des.tex, r1966

This chapter provides details of Data Encryption Standard (DES), with concepts demonstrated via a simplified, educational version called Simplified-DES. Many of the details serve mainly as reference, with little discussion.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

8.1 Overview of the Data Encryption Standard (DES)

• Symmetric block cipher
• 56-bit key, 64-bit input block, 64-bit output block
• Developed in 1977 by National Institute of Standards and Technology (NIST); designed by IBM (Lucifer) with input from National Security Agency (NSA)
• Principles used in other ciphers, e.g. 3DES, IDEA

8.2 Simplified-DES

To understand the details of a cipher, it often helps if you can perform the encryption (or decryption) steps yourself. However as common block ciphers operate on blocks of 64 bits or larger, and use similar sized keys, it is difficult to manually and efficiently perform operations. Therefore, to illustrate the principles of selected real ciphers, simplified versions have been developed. This section presents Simplified Data Encryption Standard (S-DES), which is a cut-down version of DES. For example, S-DES uses operates on 8-bit blocks, uses an 8-bit key and has only 2 rounds. As it is designed using the same principles as (real) DES but using smaller values, it is possible to step through an example encryption by hand. For some this can be a powerful way to understand the operations used in real DES. It is important however to note that S-DES is just for education; it is not a real cipher used in practice today or in the past. You will only find it referred to in textbooks and university classes.

• Input (plaintext) block: 8-bits
• Output (ciphertext) block: 8-bits
• Key: 10-bits
• Rounds: 2
• Round keys generated using permutations and left shifts
• Encryption: initial permutation, round function, switch halves
• Decryption: Same as encryption, except round keys used in opposite order

---

---

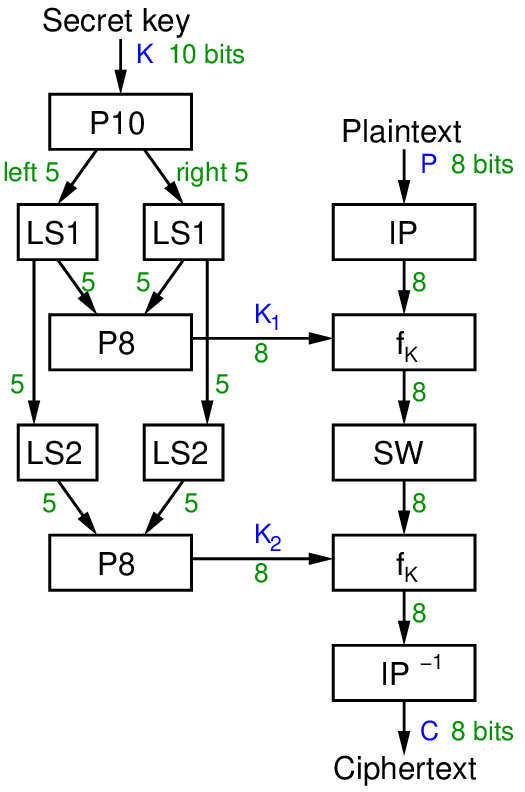
Figure 8.1 shows the key generation and encryption steps of S-DES. Key generation, shown on the left, is used to generate round keys and is the same algorithm when used for both encryption and decryption. That is, the encrypter and decrypter will generate the exact same round keys.

The encrypter started with a shared secret key 10 bits long and 8 bits of plaintext. Two sub-keys, or round keys, $K_1$ and $K_2$ are generated using the key generation steps, which involve Permutations and Left Shifts.

Encryption applies an Initial Permutation, then a round function $f_k$ (with details to be shown shortly), SWaps the two halves of the 8 bit output, then reapplies the round function, but using the 2nd round key as input. Encryption ends with the inverse of the Initial Permutation.

---

---

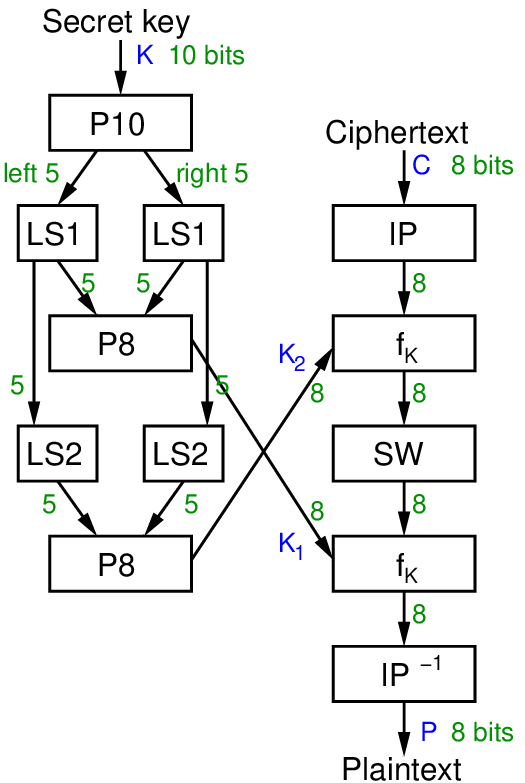
Figure 8.2 shows the key generation and decryption. Decryption is in fact identical to encryption, except the round keys are used in the opposite order. That is, for encryption round key $K_1$ is used first, then round key $K_2$. For decryption, $K_2$ is used first and then $K_1$.

---

---

Figure 8.3 shows the details of the round function, $f_k$. Note that the same steps are applied in the 2nd round, but instead $K_2$ is used as the round key. Operations include Expand and Permutate, XOR, S-boxes and a Permutation of 4 bits. The 8 bits output (left half and right half) are then input the the SWap block (swapping the two halves).

Definitions of the permutations and S-boxes follow.

As an example, permutation P4 takes a 4-bit input and produces a 4-bit output. The 1st bit of the input becomes the 4th bit of the output. The 2nd bit of the input becomes the 1st bit of the output. The 3rd bit of the input becomes the 3rd bit of the output. The 4th bit of the input becomes the 1st bit on the output.

The permutations are fixed. That is they are always these exact permutations, and known by the encrypter, decrypter and attacker.

• LS-1: left shift by 1 position
• LS-2: left shift by 2 positions
• IP${}^{-1}$: inverse of IP, such that $X={\text{IP}}^{-1}\left(\text{IP}\left(X\right)\right)$
• SW: swap the halves
• $f_K$: a round function using round key $K$
• F: internal function in each round

Video: Simplified DES Example (44 min; Jan 2016)

In summary, S-DES:

• Educational encryption algorithm
• S-DES expressed as functions:
  $$ciphertext=I{P}^{-1}\left(f_{K_2}\left(SW\left(f_{K_1}\left(IP\left(plaintext\right)\right)\right)\right)\right)$$
  $$plaintext=I{P}^{-1}\left(f_{K_1}\left(SW\left(f_{K_2}\left(IP\left(ciphertext\right)\right)\right)\right)\right)$$

• Brute force attack on S-DES is easy since only 10-bit key
• If know plaintext and corresponding ciphertext, can we determine key? Very hard

The general design of S-DES follows the same principles as DES, although the algorithm parameters differ.

• S-DES vs DES
• Block size: 8 bits vs 64 bits
• Rounds: 2 vs 16
• IP: 8 bits vs 64 bits
• F: 4 bits vs 32 bits
• S-Boxes: 2 vs 8
• Round key: 8 bits vs 48 bits

The following section presents the details of DES. This is primarily for reference (or as evidence of the similarities and differences with S-DES). You are not expected to know the details of the DES operations.

8.3 Details of DES

DES was standardised by NIST as FIPS 46, with the latest version FIPS 46-3 withdrawn as a standard in 2005. The standard contains the technical details of DES, with the main figures repeated in the following. Most (if not all) NIST standards are in the public domain.

The following figures are directly from the FIPS 46-3 PDF and are Reprinted courtesy of the National Institute of Standards and Technology, U.S. Department of Commerce. Not copyrightable in the United States. For further explanation of DES, see the standard or various textbooks (such as Stallings).

---

---

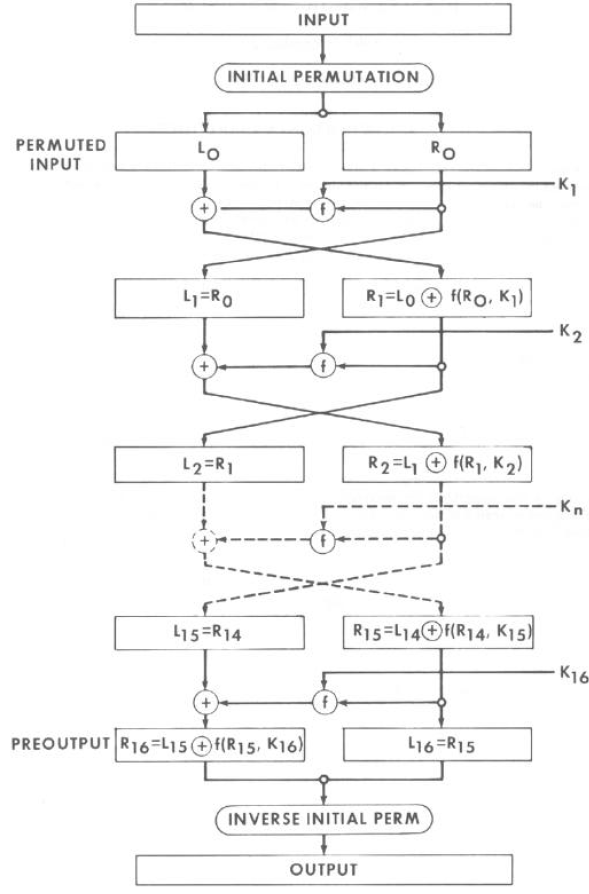
Figure 8.4 shows the overall steps in DES encryption. The details of each block are shown in the following.

---

---

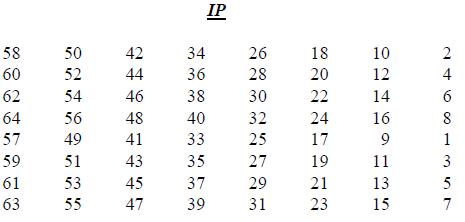
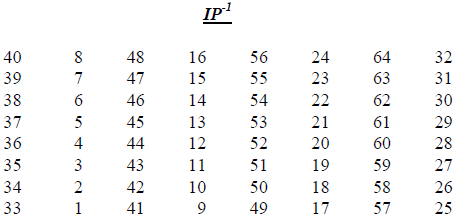
Figure 8.5 shows the initial permutation and it’s inverse. The table is read row-by-row. So the 58th input bit becomes the 1st output bit. The 50th input bit becomes the 2nd output bit. And the 7th input bit becomes the 64th output bit.

---

---

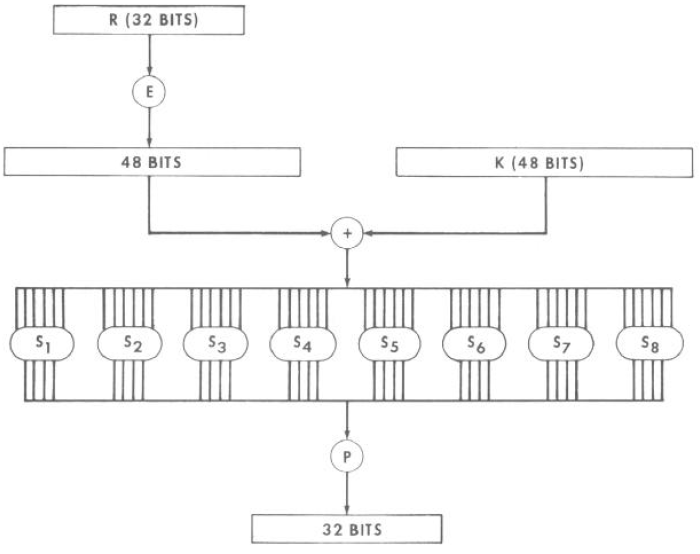
Figure 8.6 shows the details of a single round of encruption, i.e. the round function. Similar to S-DES, it takes the right half, applies an expand and permutate (E), XOR with the round key, applies S-Boxes, and then a final permutate (P).

---

---

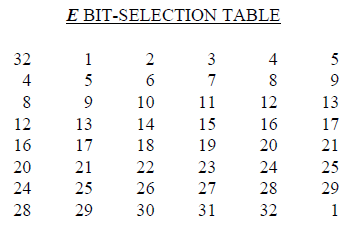
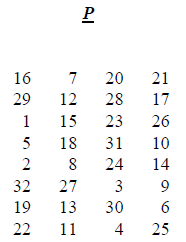
Figure 8.7 shows E and P which are used within a round of DES.

---

---

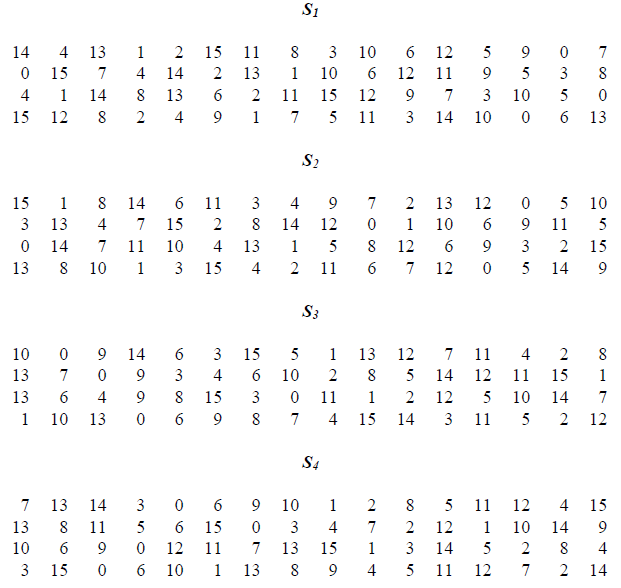
Figure 8.8 shows the first 4 S-Boxes. Each S-Box takes a 6 bit input. The first and last bit are used to determine the row, and the middle 4 bits determine the column. The result is a decimal values within the range 0 to 15, which determines the 4 bit output. See https://en.wikipedia.org/wiki/DES_supplementary_material for an example of reading the S-Boxes.

---

---

Figure 8.9 shows the last 4 S-Boxes.

---

---

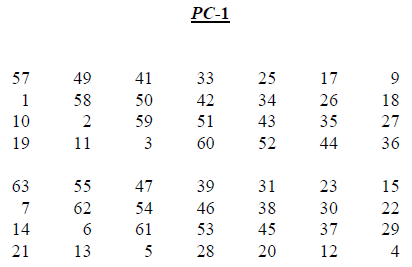
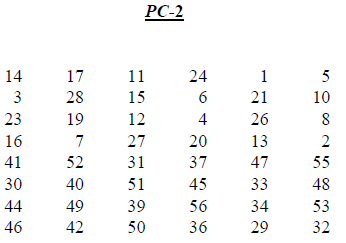
Figure 8.10 shows the Permutated Choices used in key generation.

---

---

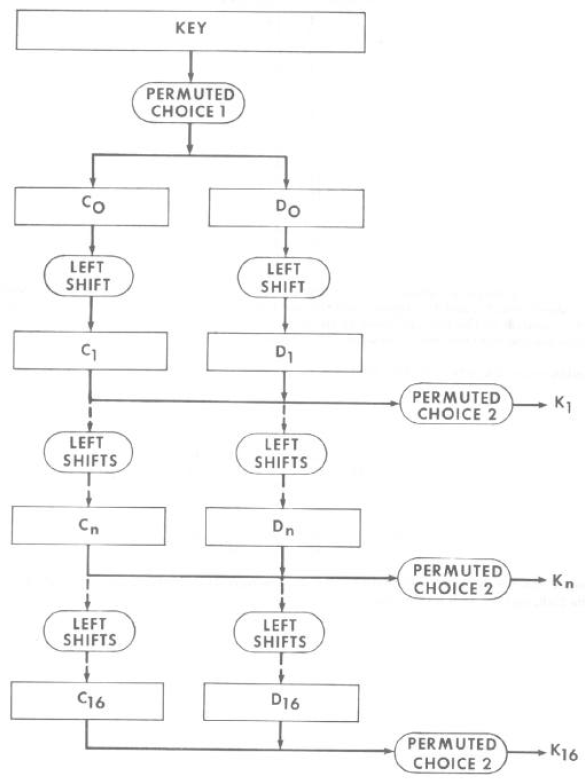
Figure 8.11 shows the overall key generation steps.

---

---

Figure 8.12 shows the schedule of left shifts indicating how many bits are shifted left when a Left Shift is applied in each round for key generation.

8.4 DES in OpenSSL

We will demonstrate several examples of using OpenSSL for DES encryption and decryption, including:

• Encrypt a file with a password using the enc operation
• Generate a random key using the rand operation
• Disable padding (with exact plaintext correct size)
• Encrypt with key and IV using enc operation
• View binary data (e.g. ciphertext) with xxd

8.4.1 DES Encryption Basics in OpenSSL

To demonstrate using OpenSSL to encrypt a file with DES, let’s create an example plaintext message. You can use any file, but for the example, let’s copy a plain text dictionary file most likely on your Linux system /usr/share/dict/words. We will name our plaintext file plaintext1.in. The file extension of .in is just to remember that this is the original plaintext input. After encrypting and decrypting, we may obtain outputs, for which we will use the extension .out. Remember, file extensions in Linux often do not matter (Chapter 4 of Network and Security in Linux explains basic Linux operations and files).

$ cp /usr/share/dict/words plaintext1.in
$ ls -l plaintext*
-rw-r--r-- 1 sgordon sgordon 938848 Jul 31 13:32 plaintext1.in

Now lets encrypt using DES. You can use the list command in OpenSSL to see the -cipher-algorithms and -cipher-commands (see Section 3.2.3). You will note there are different variants of DES, such as DES-ECB, DES-CBC and DES-CFB. The second identifier specifies the mode of operation. Modes of operation are covered in Chapter 11, but in short, these allow DES, which operates on 64-bit blocks, to be used to encrypt arbitrary sized plaintexts. The simplest mode of operation, but least secure, is Electronic Code Book (ECB). We will use ECB in this example.

Symmetric key encryption in OpenSSL is performed using the enc operation. In the simplest form, we specify the algorithm then the input file and output file (in our case, ciphertext1.bin). If we don’t specify a secret key, then OpenSSL will prompt for a password and then convert that to a secret key.

$ openssl enc -des-ecb -in plaintext1.in -out ciphertext1.bin
enter des-ecb encryption password: password
Verifying - enter des-ecb encryption password: password
$ ls -l plaintext1.in ciphertext1.bin
-rw-rw-r-- 1 sgordon sgordon 938872 Jul 31 14:15 ciphertext1.bin
-rw-r--r-- 1 sgordon sgordon 938848 Jul 31 13:32 plaintext1.in

To decrypt, include the -d option:

$ openssl enc -d -des-ecb -in ciphertext1.bin -out plaintext1.out
enter des-ecb decryption password: password
$ ls -l plaintext1.in plaintext1.out
-rw-r--r-- 1 sgordon sgordon 938848 Jul 31 13:32 plaintext1.in
-rw-rw-r-- 1 sgordon sgordon 938848 Jul 31 14:18 plaintext1.out
$ diff plaintext1.in plaintext1.out
$ xxd -l 96 ciphertext1.bin 
0000000: 5361 6c74 6564 5f5f f253 8361 b87d 1a3e  Salted__.S.a.}.>
0000010: 30ed be95 5b38 ebf9 a013 ca64 bbf4 03ea  0...[8.....d....
0000020: 3ebb cdf8 483d 5a12 acd8 bc75 140c 920b  >...H=Z....u....
0000030: da41 7376 edc3 b9bd 59c4 a5ce 0a67 408a  .Asv....Y....g@.
0000040: d23e 10ee 7ac3 f5b6 4f09 4aaf 88e4 1f96  .>..z...O.J.....
0000050: 3171 7277 91a7 100c ac04 7871 dd39 cf4c  1qrw......xq.9.L

The lack of output from the diff command indicates the files plaintext1.in and plaintext1.out are identical. We’ve retrieved the original plaintext.

xxd was used to view the first 96 bytes, in hexadecimal, of the ciphertext. The first 8 bytes contain the special string Salted__ meaning the DES key was generated using a password and a salt. The salt is stored in the next 8 bytes of ciphertext, i.e. the value f2538361b87d1a3e in hexadecimal. So when decrypting, the user supplies the password and OpenSSL combines with the salt to determine the DES 64 bit key.

Section 8.4.2 shows a more detailed example where the key and IV are specified.

8.4.2 Symmetric Key Encryption Padding and Modes of Operation

Section 8.4.1 showed a simple method for performing symmetric key encryption with OpenSSL. Now we are going to consider some more details, in particular the role of padding and modes of operation.

Recall that block ciphers, like DES and AES, operate on fixed size blocks. For example, DES encrypts a 64 bit (or 8 Byte) block of plaintext. But commonly the plaintext we want to encrypt is larger than a single block. Modes of operation, such as ECB, Cipher Block Chaining (CBC) and Counter mode (CTR), are used to apply the block cipher across multiple blocks. That is, encrypt the first 8 Bytes of plaintext with DES, then encrypt the next 8 Bytes of plaintext (or related data) with DES, and combine them together according to some algorithm. The details of modes of operation are covered in Chapter 11.

A related issue is that often the full plaintext will not be an integer multiple of blocks. For example, a 50 Byte file consists of 6 by 8 Byte blocks with 2 Bytes in the 7th block. Padding is needed to fill out that 7th block. By default, OpenSSL performs padding for you. However if you are sure you have a correct length plaintext (integer multiple of blocks), you can omit padding. This is useful to perform simple exploration of the output.

The following shows an example of using OpenSSL without padding, and demonstrates the weakness of the ECB mode of operation.

To get started, we need a plaintext message to encrypt. The first command below generates a message (saving to a file), and the subsequent commands show us some information about the message/file.

$ echo -n "Hello. This is our super secret message. Keep it secret please. Goodbye." > plaintext.txt
$ cat plaintext.txt 
Hello. This is our super secret message. Keep it secret please. Goodbye.
$ wc -m plaintext.txt 
72 plaintext.txt
$ ls -l
total 4
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:39 plaintext.txt
$ xxd -c 8 plaintext.txt 
0000000: 4865 6c6c 6f2e 2054  Hello. T
0000008: 6869 7320 6973 206f  his is o
0000010: 7572 2073 7570 6572  ur super
0000018: 2073 6563 7265 7420   secret
0000020: 6d65 7373 6167 652e  message.
0000028: 204b 6565 7020 6974   Keep it
0000030: 2073 6563 7265 7420   secret
0000038: 706c 6561 7365 2e20  please.
0000040: 476f 6f64 6279 652e  Goodbye.
$ xxd -b -c 8 plaintext.txt 
0000000: 01001000 01100101 01101100 01101100 01101111 00101110 00100000 01010100  Hello. T
0000008: 01101000 01101001 01110011 00100000 01101001 01110011 00100000 01101111  his is o
0000010: 01110101 01110010 00100000 01110011 01110101 01110000 01100101 01110010  ur super
0000018: 00100000 01110011 01100101 01100011 01110010 01100101 01110100 00100000   secret
0000020: 01101101 01100101 01110011 01110011 01100001 01100111 01100101 00101110  message.
0000028: 00100000 01001011 01100101 01100101 01110000 00100000 01101001 01110100   Keep it
0000030: 00100000 01110011 01100101 01100011 01110010 01100101 01110100 00100000   secret
0000038: 01110000 01101100 01100101 01100001 01110011 01100101 00101110 00100000  please.
0000040: 01000111 01101111 01101111 01100100 01100010 01111001 01100101 00101110  Goodbye.

The meaning of the preceding output is:

1. Create a short text message with echo. The -n option is used to ensure no newline is added to the end. There are two things about this message that will be important later: the length is a multiple of 8 characters (9 by 8 characters) and the word secret appears twice (in particular positions).
2. Display the message on the screen with cat.
3. Count the number of characters with wc.
4. View the file size with ls.
5. Show the message in hexadecimal and binary using xxd. From now on, we’ll only look at the hexadecimal values (not binary).

To encrypt with DES-ECB we need a secret key (as well as IV). You can choose your own values. For security, they should be randomly chosen. We saw in Chapter 3 different ways to generate random values. Let’s use OpenSSL’s rand twice: the first will be for the secret key and the second for the IV.

$ openssl rand -hex 8
001e53e887ee55f1
$ openssl rand -hex 8
a499056833bb3ac1

Now encrypt the plaintext using DES-ECB. The IV and Key are taken from the outputs OpenSSL PRNG above. Importantly, we use the -nopad option at the end:

$ openssl enc -des-ecb -e -in plaintext.txt -out ciphertext.bin -iv a499056833bb3ac1 -K 001e53e887ee55f1 -nopad

Now look at the output ciphertext. First note it is the same length as the plaintext (as expected, when no padding is used). And on initial view, the ciphertext looks random (as expected). But closer inspection you see there is some structure: the 4th and 7th lines of the xxd output are the same. This is because it corresponds to the encryption of the same original plaintext " secure " (recall that word was repeated in the plaintext, in the positions such that it is in a 64-bit block). Since ECB is used, repetitions in input plaintext blocks will result in repetitions in output ciphertext blocks. This is insecure (especially for long plaintext). Another mode of operation, like CBC, should be used.

$ ls -l
total 8
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:42 ciphertext.bin
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:39 plaintext.txt
$ xxd -c 8 ciphertext.bin
0000000: 56dc b368 d9ef 0793  V..h....
0000008: 7be4 a87d e26d c2f1  {..}.m..
0000010: e042 bbe6 9e00 6d37  .B....m7
0000018: f1e9 7163 cb4a 38d8  ..qc.J8.
0000020: 5394 a92f 8cf2 ac72  S../...r
0000028: 5064 be07 f67c d807  Pd...|..
0000030: f1e9 7163 cb4a 38d8  ..qc.J8.
0000038: a31c 0efd cd0b dd03  ........
0000040: 0486 7e2d 00ad 762d  ..~-..v-

Now lets decrypt:

$ openssl enc -des-ecb -d -in ciphertext.bin -out received.txt -iv a499056833bb3ac1 -K 001e53e887ee55f1 -nopad

And look at the decrypted value. Of course, it matches the original plaintext message.

$ ls -l
total 12
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:42 ciphertext.bin
                                                                                                                                                  
                                                                                                                                                  
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:39 plaintext.txt
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:43 received.txt
$ cat received.txt 
Hello. This is our super secret message. Keep it secret please. Goodbye.
$ xxd -c 8 received.txt 
0000000: 4865 6c6c 6f2e 2054  Hello. T
0000008: 6869 7320 6973 206f  his is o
0000010: 7572 2073 7570 6572  ur super
0000018: 2073 6563 7265 7420   secret
0000020: 6d65 7373 6167 652e  message.
0000028: 204b 6565 7020 6974   Keep it
0000030: 2073 6563 7265 7420   secret
0000038: 706c 6561 7365 2e20  please.
0000040: 476f 6f64 6279 652e  Goodbye.

Now lets try and decrypt again, but this time using the wrong key. I’ve changed the last hexadecimal digit of the key from “1” to “2”.

$ openssl enc -des-ecb -d -in ciphertext.bin -out received2.txt -iv a499056833bb3ac1 -K 001e53e887ee55f2 -nopad

Looking at the decrypted message, it is random. We didn’t obtain the original plaintext. Normally, when padding is used, OpenSSL adds a checksum when encrypting which allows, after decrypting, incorrect deciphered messages to be automatically detected.

$ ls -l
total 16
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:42 ciphertext.bin
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:39 plaintext.txt
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:46 received2.txt
-rw-r--r-- 1 sgordon sgordon 72 Nov 11 16:43 received.txt
$ xxd -c 8 received2.txt 
0000000: 0346 e59e c22d 403f  .F...-@?
0000008: 63ff 28fd eb6b 387d  c.(..k8}
0000010: b52f d595 06c0 342f  ./....4/
0000018: f419 3569 e383 c857  ..5i...W
0000020: 0a77 0b49 6f62 cb64  .w.Iob.d
0000028: 8265 d419 51f3 ea12  .e..Q...
0000030: f419 3569 e383 c857  ..5i...W
0000038: f296 33f3 5cf4 d359  ..3.\..Y
0000040: e205 4018 0ce0 34f5  ..@...4.

However the checksum used within OpenSSL is not perfect, so it shouldn’t be relied upon for secure authentication (i.e. checking the received message is correct). Chapter 17 discusses different ways for the receiver to be sure they have obtained the original message.

Video: DES Encryption using OpenSSL (13 min; Jan 2012)

8.4.3 DES OpenSSL Exercises

8.5 DES in Python

The Python Cryptography library includes symmetric key encryption using various algorithms. DES is covered under TripleDES. That is, using TripleDES with a 64 bit key is equivalent to using DES. See the examples for generic symmetric encryption at:

• cryptography.io/en/latest/hazmat/primitives/symmetric-encryption/