15 Elliptic Curve Cryptography

Chapter 15
Elliptic Curve Cryptography

15.1 Overview of Elliptic Curve Cryptography
15.2 Applications of Elliptic Curve Cryptography
15.3 Elliptic Curve Cryptography in OpenSSL

RSA (Chapter 13) and Diffie-Hellman (Chapter 14) are two widely-used public key cryptography algorithms. Their security depends on the difficulty of factoring large integers into primes and solving discrete logarithms for integers, respectively. Their problem however is that keys are relatively large (e.g. 2048-bits for RSA). This leads to high communications overhead when exchanging keys in security protocols, and possibly performance limitations when implementing on low-cost computers.

Elliptic Curve Cryptography (ECC) is another, newer approach to public key cryptography. Mathematical operations are performed on an elliptic curve, where some operations can be easy if certain values are known, but practically impossible of those values are unknown. This is similar to the integer factorisation and discrete logarithm problems that make RSA and Diffie-Hellman secure. In fact, the problem is solving a discrete logarithm on an elliptic curve (rather than for integers as in Diffie-Hellman).

The main benefit of ECC is in performance. Specifically to achieve similar level of security as RSA and Diffie-Hellman, ECC has much smaller key sizes: 100’s of bits vs 1000’s of bits. Chapter 18 gives common recommended key lengths for RSA, Diffie-Hellman and ECC. In the past, RSA and (normal) Diffie-Hellman were favoured as ECC was relatively new. But now ECC is used in many applications, e.g. secret key exchange regularly uses the elliptic curve form of Diffie-Hellman rather than the normal, integer-based form¹ ¹When referring to “Diffie-Hellman”, we normally mean the algorithm based on integer discrete logarithms. However there is a Diffie-Hellman algorithm based on elliptic curve discrete logarithms. We will refer to this as “ECDH”. .

This chapter gives a brief, as simple-as-possible, introduction to ECC.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

15.1 Overview of Elliptic Curve Cryptography

This section steps through the maths of elliptic curves, and explains why operations on an elliptic curve can be used for public key cryptography.

Definition 15.1 (Elliptic Curve). An elliptic curve is defined by:

y^{2} = x^{3} + a x + b

(with some constraints of constants $a$ and $b$ )

The constraints on $a$ and $b$ specify the relationship between the values, i.e. you cannot necessarily choose any values. We will not go into that detail here.

Credit: Generated based on MIT Licensed code by Fang-Pen Lin

Figure 15.1: Elliptic Curve for

y^{2} = x^{3} - 3 x + 5

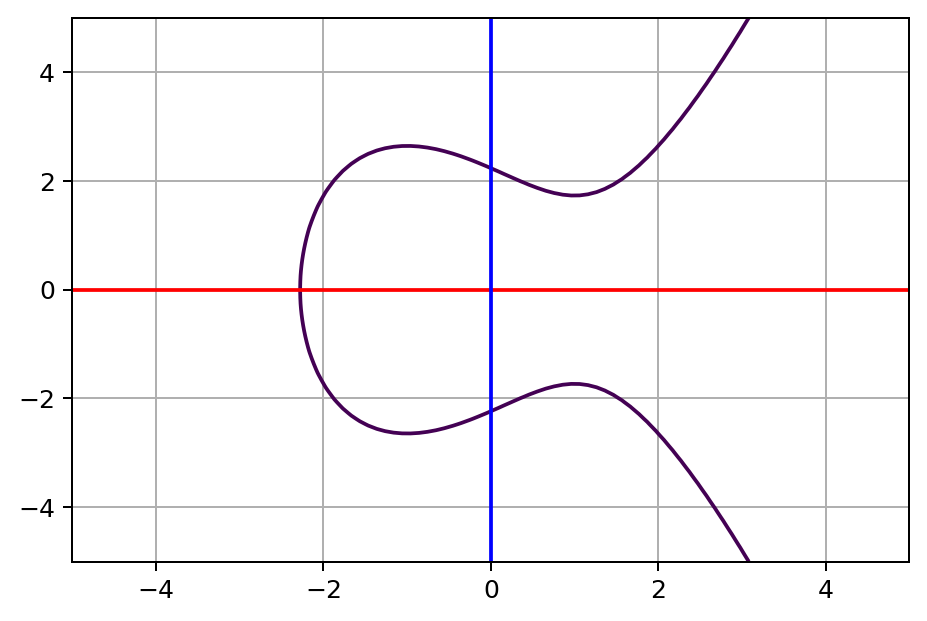
Figure 15.1 shows an example elliptic curve where $a = - 3$ and $b = 5$ , plotted for $x$ values from -4 to 4. An elliptic curve always mirrors itself about the horizontal (red) axis.

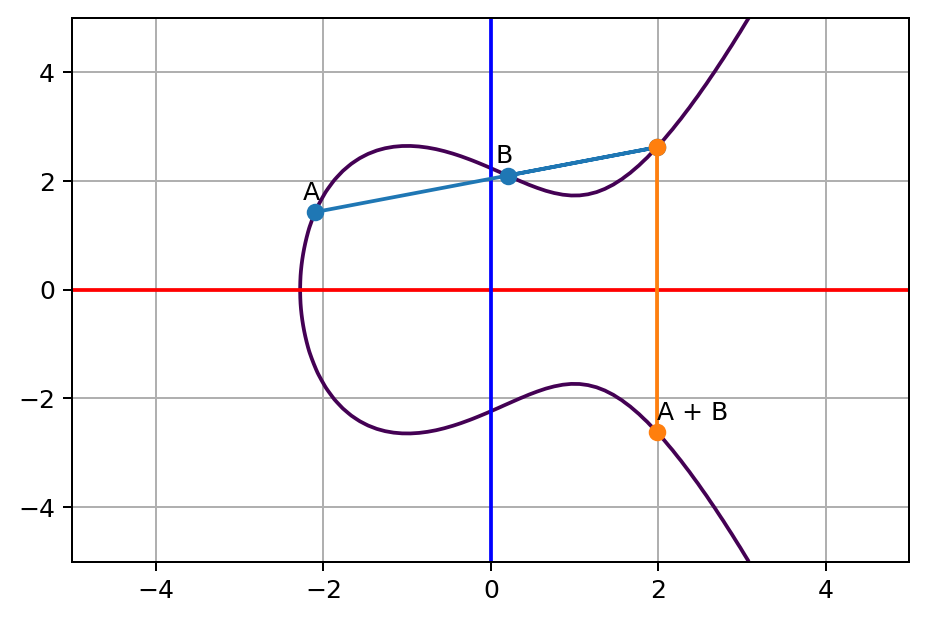
Definition 15.2 (Addition Operation with an Elliptic Curve). Select two points on the curve, A and B, and draw a straight line through them. The line will intersect with the curve at a third point, R (and no other points). The horizontal inverse of point R, is defined as the addition of A and B.

A + B = - R

See the following figure for an example of this concept. Note the points, A, B, R and -R are just $(x, y)$ coordinates.

Credit: Generated based on MIT Licensed code by Fang-Pen Lin

Figure 15.2: Addition Operation on Elliptic Curve

Figure 15.2 shows the concept of addition. Adding the points A and B results in the point shown as A+B. There is always a third point that intersects the curve on the line between A and B, and there is always an inverse of this point.

Note that we could continue the addition. For example, with A+B, add another point C, to arrive at a new point A+B+C. And so on.

Rather than adding two different points, we can simply add a single point to itself. The same concepts apply.

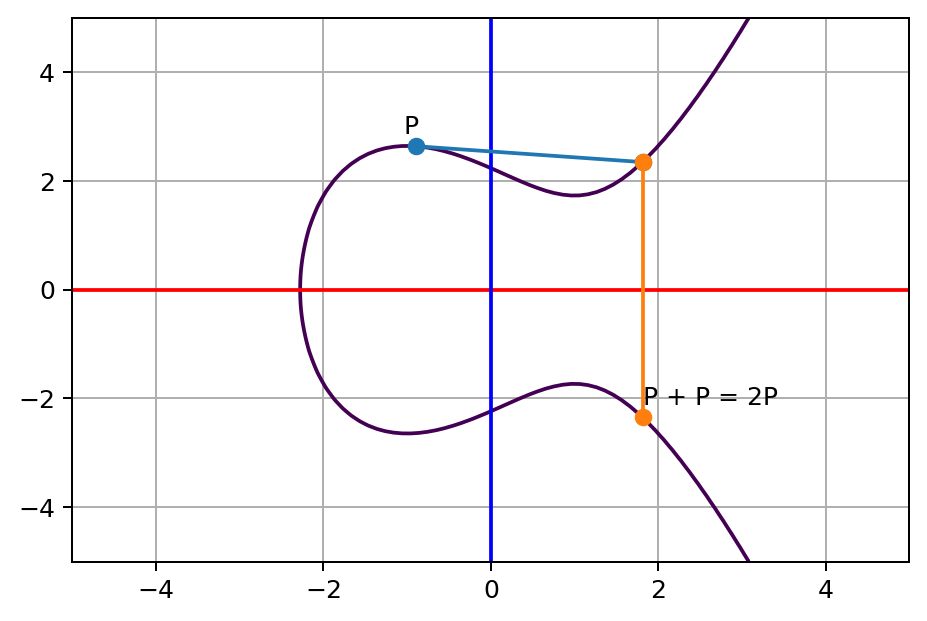
Credit: Generated based on MIT Licensed code by Fang-Pen Lin

Figure 15.3: Self Addition on Elliptic Curve

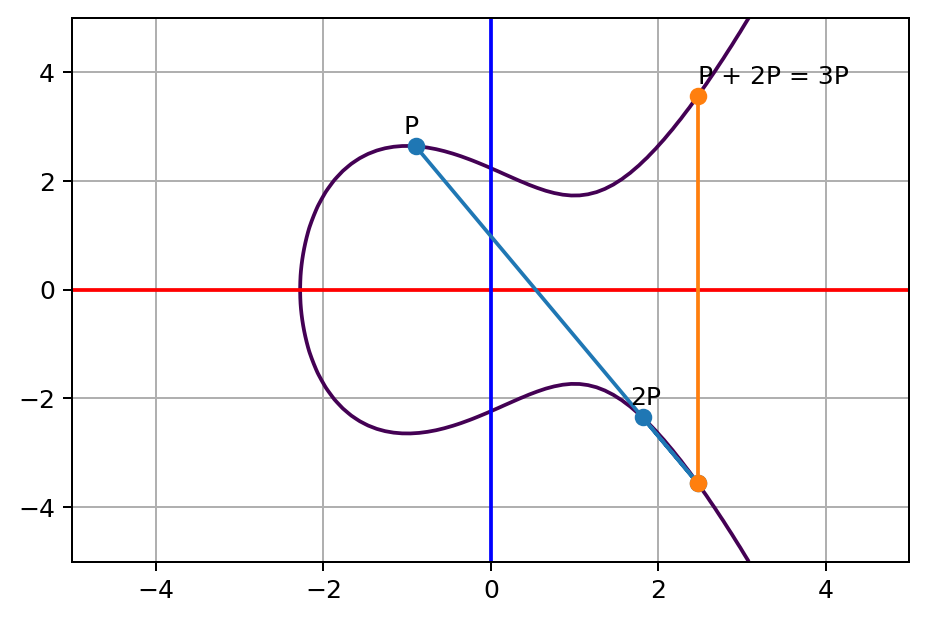
Figure 15.3 shows the self addition of point P. When adding a single point P to itself, the line that intersects P is chosen as the line tangent to P. So P+P = 2P.

We can continue to add P.

Credit: Generated based on MIT Licensed code by Fang-Pen Lin

Figure 15.4: P + 2P on Elliptic Curve

Figure 15.4 shows P + 2P = 3P. Then we can add P again to get 4P and so on.

Credit: Generated based on MIT Licensed code by Fang-Pen Lin

Figure 15.5: NP on Elliptic Curve

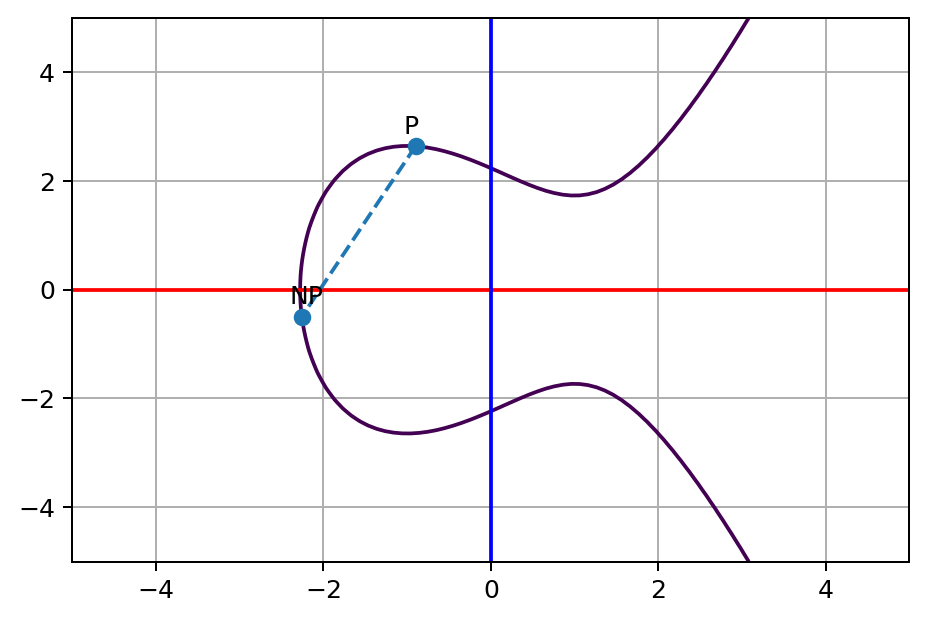
Figure 15.5 shows NP. In this example N=13. That is, we start with point P, and add P twelve times, resulting in the point 13P.

So now we know the concept of point addition on an elliptic curve, how can that be used for cryptography?

User chooses a point $P$ (global public parameter)
User chooses a large, random $N$ (private key)
User calculates NP (public key)
- Easy, since there is a shortcut (described shortly)
Challenge for attacker: given NP, find N
- Computationally hard for large $N$

As with other public key systems, elliptic curve cryptography relies on the fact that it is easy for the user to generate the public and private key, but practically impossible for an attacker to find the private key from the public key.

Why is that the case? So far we said $N P$ is found by adding $P$ $N - 1$ times, that is, takes $N - 1$ addition operations. So an attacker could simply start with $P$ , and keep adding $P$ until they get an answer of $N P$ . Now the know how many additions, i.e. the private value $N$ .

However if $N$ is large enough the attackers method will be practically impossible. And for the user to generate $N P$ when they know $N$ , there is a shortcut that is practically achievable.

Assume $N$ is large, e.g. 256-bit random number
Naive point addition: $P + P + P + P + \dots + P + P$ ( $2^{256} - 1$ additions)
Shortcut algorithm for point addition:
- Calculate $P$ , $P + P = 2 P = 2^{1} P$ , $2 P + 2 P = 4 P = 2^{2} P$ , $4 P + 4 P = 8 P = 2^{3} P$ , …, $2^{255} P$ (255 additions)
- Write N as binary expansion, e.g.:
  - $N = 233 = 2^{7} + 2^{6} + 2^{5} + 2^{3} + 2^{0}$
  - $N P = 2^{7} P + 2^{6} P + 2^{5} P + 2^{3} P + 2^{0} P$
  - In this example, there are 4 point additions
  - Maximum number of point additions for 256-bit $N$ is 255
- Calculate $N P$ using the binary expansion
- Maximum number of point additions for 256-bit $N$ : 255 + 255 = 510
If $N$ is 256-bit random number:
Attacker: $\approx 2^{256}$ point additions (practically impossible)
User: $\approx 2 \times 256$ point additions (easy)

In summary, knowing the $b$ -bit value $N$ , the user needs to perform about $2 \times b$ point additions. This is easy. But the attacker, who doesn’t know $N$ , must perform about $2^{b}$ point additions, which is practically impossible.

The above discussed a normal elliptic curve
But to ensure all values contained within finite coordinate space, modular arithmetic is used
$y^{2} mod p = (x^{3} + a x + b) mod p$
$p$ is a prime number

The figures and examples given previously shown an elliptic curve without modular arithmetic. But in elliptic curve cryptography, modular arithmetic occurs. The same principles, and reasoning why it is hard for the attacker, still apply. The plots of the elliptic curve in modular arithmetic look different however—they now have distinct points in a finite coordinate space. Search online for examples.

Next we will see how elliptic curves are applied to build cryptographic mechanisms.

15.2 Applications of Elliptic Curve Cryptography

ECC can be applied for various cryptographic mechanisms:

Secret key exchange, e.g. ECDH, ECMQV
Digital signatures, e.g. ECDSA, EC-KCDSA
Public key encryption, e.g. ECIES, PSEC

The most common applications are for secret key exchange, especially with Elliptic Curve Diffie-Hellman (ECDH), and digital signatures with Elliptic Curve Digital Signature Algorithm (ECDSA). We will look at ECDH in the following.

Algorithm 15.1 (Elliptic Curve Diffie-Hellman Key Exchange). Assume users $A$ and $B$ have EC key pairs: $P U_{A} = N P$ , $P R_{A} = N$ , $P U_{B} = M P$ , $P R_{B} = M$ .

User $A$ calculates secret $S_{A} = N \cdot P U_{B} = N M P$ using shortcut point addition.
User $B$ calculates secret $S_{B} = M \cdot P U_{A} = M N P$ using shortcut point addition.

Diffie-Hellman key exchange can be used using ECC so that both users obtain a shared secret over an insecure channel. Users agree on a public point $P$ . They generate their own keypairs, where the private key is some large random number, and the public key is that number times $P$ . Note that in the key generation, each user can use the shortcut to calculate $N P$ or $M P$ .

Assume the users exchange public keys. They then use their own private key multiplied by the other’s public key. Again, the shortcut point addition can be used. Both will arrive at the same point (coordinate), i.e. $N M P = M N P$ . This is the shared secret.

An attacker that knows the public keys and initial point $P$ has to find either $N$ or $M$ . If those numbers are large enough, this is practically impossible.

Until now we have referred to general or example elliptic curves without specifying the parameter values. In practice, users of ECC do not select their own parameters, but rather use standardised parameters.

Parameters for ECC are usually standardised
- Base point, $P$ (also referred to as generator, $G$ )
- Curve parameters, $a$ and $b$
- Prime, $p$
- Other parameters also included
Common curves (see also https://safecurves.cr.yp.to/):
- NIST FIPS 186: P-256, P-384 and 13 others
- SECG: secp160k1, secp160r1, …(NIST curves are a subset)
- ANSI X9.62: prime192, prime256, …
- Other curves: Curve25519, Brainpool

SECG in SEC 2 defined a large set of curves. The NIST curves were a subset of the SEC 2 curves. NSA Suite B curves are a subset of NIST curves.

15.3 Elliptic Curve Cryptography in OpenSSL

In OpenSSL, the ecparam command is used for elliptic curve cryptography parameter and key generation. Many of the operations are explained the OpenSSL Command Line Elliptic Curve Operations wiki. You can list the curves supported by OpenSSL:

alice@node1:~$ openssl ecparam -list_curves
  secp112r1 : SECG/WTLS curve over a 112 bit prime field
  secp112r2 : SECG curve over a 112 bit prime field
  secp128r1 : SECG curve over a 128 bit prime field
  secp128r2 : SECG curve over a 128 bit prime field
  ...
  brainpoolP512r1: RFC 5639 curve over a 512 bit prime field
  brainpoolP512t1: RFC 5639 curve over a 512 bit prime field
  SM2       : SM2 curve over a 256 bit prime field

For a selected curve, you can see the detailed parameters. For example, for the secp256k1 curve:

alice@node1:~$ openssl ecparam -name secp256k1 -text -param_ecn explicit -noout
Field Type: prime-field
Prime:
     00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:
     ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:fe:ff:
     ff:fc:2f
A:    0
B:    7 (0x7)
Generator (uncompressed):
                                                                                                                                                  
                                                                                                                                                  
     04:79:be:66:7e:f9:dc:bb:ac:55:a0:62:95:ce:87:
     0b:07:02:9b:fc:db:2d:ce:28:d9:59:f2:81:5b:16:
     f8:17:98:48:3a:da:77:26:a3:c4:65:5d:a4:fb:fc:
     0e:11:08:a8:fd:17:b4:48:a6:85:54:19:9c:47:d0:
     8f:fb:10:d4:b8
Order:
     00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:
     ff:fe:ba:ae:dc:e6:af:48:a0:3b:bf:d2:5e:8c:d0:
     36:41:41
Cofactor:  1 (0x1)

Public/private key pairs can be generated from named curve (e.g. secp256k1) or by first outputting curve parameters to a file. Here we will show the latter:

alice@node1:~$ openssl ecparam -name secp256k1 -out secp256k1.pem
alice@node1:~$ openssl ecparam -in secp256k1.pem -genkey -noout -out alice-k
ey.pem

Alternatively, you could combine the above two commands into a single, by specifying the -name of the curve rather than the -in file. The OpenSSL Command Line Elliptic Curve Operations wiki explains the different options, as well as ensuring parameters are in a format that can be used by different versions of OpenSSL.

Once the curve parameters file (e.g. secp256k1.pem is generated, you can use the genpkey, key and pkeyutl operations in a similar manner as with Diffie-Hellman in Section 14.5.

[prev] [prev-tail] [front] [up]

Chapter 15Elliptic Curve Cryptography

15.1 Overview of Elliptic Curve Cryptography

15.2 Applications of Elliptic Curve Cryptography

15.3 Elliptic Curve Cryptography in OpenSSL

Chapter 15
Elliptic Curve Cryptography