14 Diffie–Hellman Key Exchange

Chapter 14
Diffie–Hellman Key Exchange

14.1 Diffie–Hellman Key Exchange Algorithm
14.2 Analysis of DHKE
14.3 Man-in-the-Middle Attack on DHKE
14.4 Implementations of DHKE
14.5 Diffie–Hellman in OpenSSL
14.6 DHKE in Python

File: crypto/dh.tex, r1968

This chapter presents the Diffie–Hellman key exchange algorithm, which was the first example of public key cryptography.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

14.1 Diffie–Hellman Key Exchange Algorithm

Whitfield Diffie and Martin Hellman, along with Ralph Merkle, were the first to publish algorithms for public key cryptography. Their algorithm was designed to exchange a secret key between two parties, and commonly referred to as Diffie-Hellman Key Exchange (DHKE). You can read more about Diffie, Hellman and Merkle in Chapter C.

Diffie and Hellman proposed public key cryptosystem in 1976
- Motivation: solve the problem of how to exchange secret keys for symmetric key crypto
- Proposed protocol for exchanging secrets using public keys
- Merkle also contributed to the idea; sometimes called Diffie–Hellman-Merkle key exchange
DHKE is algorithm for exchanging secret key (not for secrecy of data)
- E.g. two users want to use symmetric key crypto, but need to first exchange a secret key
Based on discrete logarithms
- Easy to calculate exponential modulo a prime
- Infeasible to calculate inverse, i.e. discrete logarithm

It is important to note that DHKE is a “key exchange” protocol. The purpose is for two users to exchange a secret key. Once a secret key has been exchanged with DHKE, the two users can then use that secret key for other purposes (e.g. for encrypting data using AES).

If you do not know what a discrete logarithm is, it is worth refreshing your knowledge in number theory from Chapter 5.

Algorithm 14.1 (Diffie–Hellman Key Exchange). One-time setup. A and B agree upon public values prime $p$ and generator $g$ , where $g < p$ and $g$ is a primitive root of $p$ .

Protocol.

A: select private $P R_{A} < p$
A: calculate public $P U_{A} = g^{P R_{A}} mod p$
A $\to$ B: send $P U_{A}$
B: select private $P R_{B} < p$
B: calculate public $P U_{B} = g^{P R_{B}} mod p$
B: calculate secret $K_{B} = P U_{A}^{P R_{B}} mod p$
B $\to$ A: send $P U_{B}$
A: calculate secret $K_{A} = P U_{B}^{P R_{A}} mod p$

Result. $K_{A} = K_{B}$ is the shared secret value

The values $p$ and $g$ are either agreed upon in advance, or selected by one user and sent to the other in the first message. Both values are public; the attacker is assumed to know them.

When two users need to exchange a shared secret, one of them initiates the protocol. User A and B actually perform the same steps, but just with different values. First a private value $P R$ is randomly selected. Then a public value $P U$ is calculated. Both users exchange their public $P U$ values (and the attacker may learn them). Finally, both users calculate their private values $K$ based on their own $P R$ and received $P U$ . The values and calculations are designed such that the $K$ calculated by each user will be the same. $K$ is the shared secret key.

Note that the parameters have different variables or names in different sources. You may also see:

prime $p$ : $q$
generator $g$ : $α$
private $P R_{A}$ and $P R_{B}$ : $X_{A}$ and $X_{B}$ ; or $a$ and $b$ ; or $x$ and $y$
public $P U_{A}$ and $P U_{B}$ : $Y_{A}$ and $Y_{B}$ ; or $A$ and $B$ ; or $e$ and $f$
secret $K$ : $s$

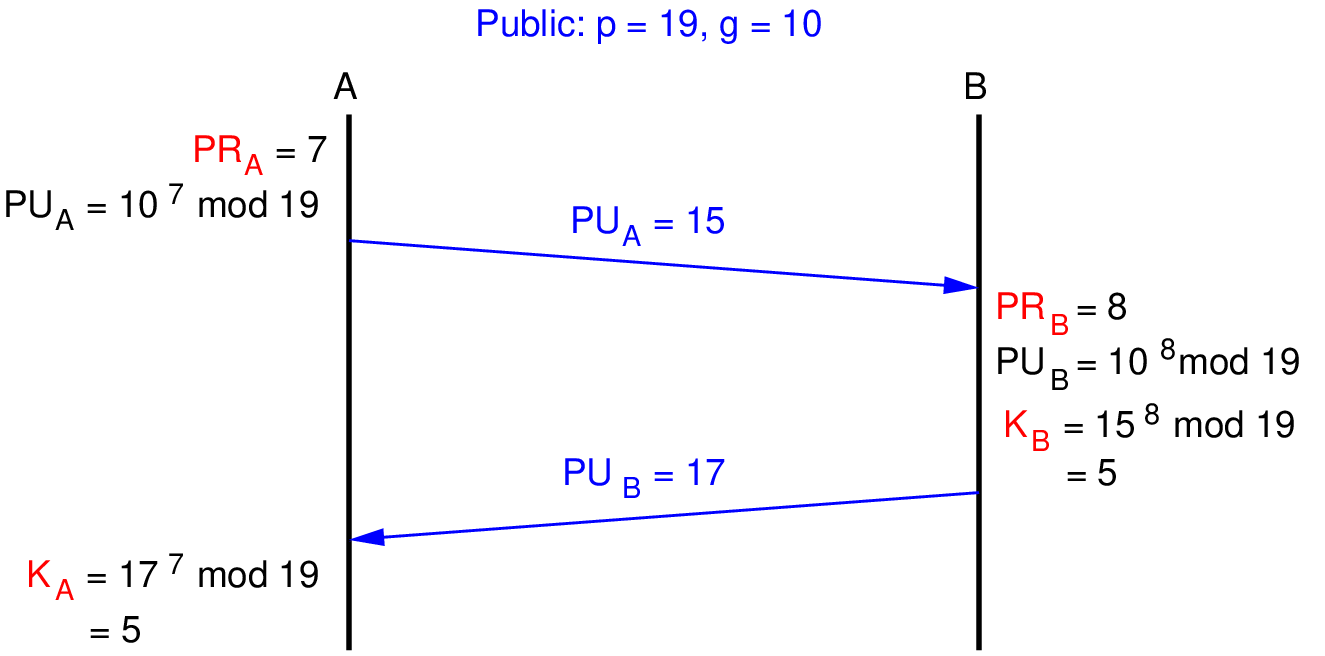
Exercise 14.1 (Diffie–Hellman Key Exchange). Assume two users, A and B, have agreed to use DHKE with prime $p = 19$ and generator $g = 10$ . Assuming A randomly chose private $P R_{A} = 7$ and B randomly chose private $P R_{B} = 8$ , find the shared secret key.

Solution 14.1 (Diffie–Hellman Key Exchange). First note that $g = 10$ is in indeed a primitive root of $p = 19$ , as seen in the examples on number theory in Section 5.4. That is, $1 0^{0}$ , $1 0^{1}$ , $1 0^{2}$ , $1 0^{3}$ , $\dots$ , $1 0^{18}$ give distinct values in mod 19.

Let’s consider the first phase from user A’s perspective. A chooses private value $P R_{A} = 7$ , which is less than 19. Then A calculates their public value:

\begin{array}{rcl} P U_{A} & = & g^{P R_{A}} mod p \\ = & 1 0^{7} mod 19 \\ = & 10000000 mod 19 \\ = & 15 \end{array}

A sends $P U_{A} = 15$ to B.

Now consider from user B’s perspective. B calculates their public value using their chosen $P R_{B} = 8$ ::

\begin{array}{rcl} P U_{B} & = & g^{P R_{B}} mod p \\ = & 1 0^{8} mod 19 \\ = & 100000000 mod 19 \\ = & 17 \end{array}

B sends $P U_{B} = 17$ to A.

B can also calculate their version of the shared secret:

\begin{array}{rcl} K_{B} & = & P U_{A}^{P R_{B}} mod p \\ = & 1 5^{8} mod 19 \\ = & 2562890625 mod 19 \\ = & 5 \end{array}

As A has received B’s public value, A can also calculate their version of the shared secret:

\begin{array}{rcl} K_{A} & = & P U_{B}^{P R_{A}} mod p \\ = & 1 7^{7} mod 19 \\ = & 410338673 mod 19 \\ = & 5 \end{array}

In summary, A and B have exchanged public values and then calculated a shared secret key of $K = 5$ . Figure 14.1 illustrates the DHKE steps.

Figure 14.1: Diffie–Hellman Key Exchange Example

Video: Diffie-Hellman Key Exchange with Example (18 min; Mar 2015)

14.2 Analysis of DHKE

Same shared secret: $K_{A}$ and $K_{B}$ must be identical
Computational efficiency: Easy to calculate $P U$ and $K$
Secure: Infeasible to determine PR or K from known values
- Attacker knows 3 public values in $P U_{A} = g^{P R_{A}} mod p$
- Must be practically impossible to find the 4th value $P R_{A}$

While we don’t show it here, it can easily be proved that DHKE will produce the same value of $K$ for both users.

Modular exponentiation, while slow with big numbers, is easy to calculate, i.e. can be achieved in less than seconds.

The inverse operation of modular exponentiation, referred to as a discrete logarithm, is hard to calculate. With large enough values, it is considered impossible to calculate.

Question 14.1 (Prove Identical Keys in DHKE). Prove that user A and user B will always calculate the same shared secret key in DHKE. That is, prove that $K_{A} = K_{B}$ .

Video: Proof of Identical Keys in DHKE (5 min; Mar 2015

Question 14.2 (Brute Force Attack on PR in DHKE). Assuming you have intercepted $P U_{A} = 15$ from the DHKE exercise, how would you perform a brute force attack to find $P R_{A}$ ? How could such a successful brute force attack be prevented in practice?

Exercise 14.2 (Discrete Logarithm Attack in DHKE). Assuming a brute force attack is not possible, write an equation that the attacker would have to solve to find $P R_{A}$ .

Solution 14.2 (Discrete Logarithm Attack in DHKE). Consider the equation:

P U_{A} = g^{P R_{A}} mod p

There is one unknown variable in the equation of four variables. The equation consists of modular exponentiation. The inverse operation is modular logarithm, or more commonly discrete logarithm, which can be written as:

P R_{A} = {dlog}_{g, p} (P U_{A})

which can be read as “given the base $g$ and modulus $p$ , find the index (or exponent) $P R_{A}$ that produces the result $P U_{A}$ ”.

Discrete Logarithm Problem: $given g, p and g^{x} mod p, find x$
For certain values of p, considered computationally hard
- $p$ is a safe prime, i.e. $p = 2 q + 1$ where $q$ is a large prime
- $p$ is very large, usually at least 1024 bits
2016: Discrete logarithm with 768 bit prime $p$ was solved within 5300 core years on 2.2GHz Xeon E5-2660 processor
Considered harder to solve than equivalent integer factorisation
- 768 bit integer factored in 2000 core years

14.3 Man-in-the-Middle Attack on DHKE

A very practical attack on DHKE is a Man-in-the-Middle (MITM) attack. If an attacker has the ability to intercept and send messages in between the two users, and the messages have no form of authentication, this attack can be successful.

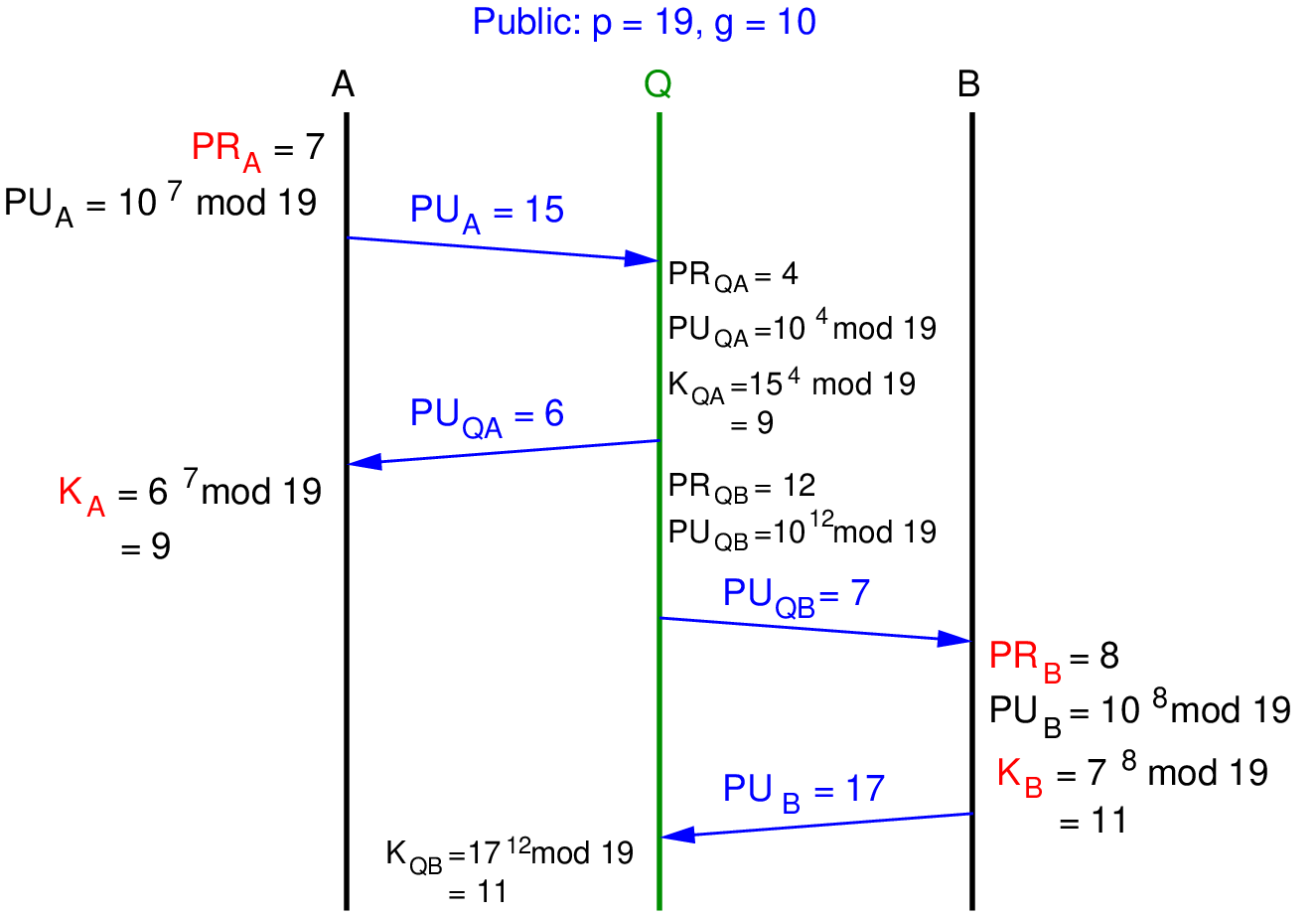
Exercise 14.3 (MITM Attack on DHKE). Consider the “Diffie–Hellman Key Exchange” exercise where user A chooses $P R_{A} = 7$ and B chooses $P R_{B} = 8$ . Show how a MITM can be performed such that an attacker Q can decrypt any communications between A and B that use the secret shared between A and B.

Solution 14.3 (MITM Attack on DHKE). In a MITM attack, the attacker Q intercepts messages between A and B, and masquerades as A to B, and as B to A. So when A sends its public value $P U_{A}$ to B, it is intercepted by Q. Q then masquerades as B: selecting it’s own $P R_{Q A}$ , calculating a $P U_{Q A}$ and sending back to A. A and Q calculate a shared secret key which will be identical. Without authentication of messages, A thinks it is communicating with B (since it send a message to B, and received a reply from who they think is B).

Q then performs a DHKE with B, and B thinks this is with A. The end result is that A and Q have a shared secret, and B and Q have another shared secret, and both A and B think their shared secret is with each other.

Figure 14.2 illustrates the MITM, where Q chooses random private value $P R_{Q A} = 4$ for the DHKE with A and $P R_{Q B} = 12$ for the DHKE with B.

Figure 14.2: Diffie–Hellman MITM Attack Example

Now assuming the shared secrets are used as a key in a symmetric key cipher. When A encrypts a message and sends to B, Q can intercept and decrypt, since Q knows A’s shared secret (9). Q can then encrypt the message with B’s shared secret (11) and send on to B. B receives and decrypts, and subsequently responds to A. The exchange of encrypted data continues between A and B, without them noticing that Q is intercepting and decrypting the data.

Video: Man-in-the-Middle Attack on Diffie-Hellman Key Exchange (16 min; Mar 2015)

14.4 Implementations of DHKE

Some (older) communication protocols defined a fixed value of p and g
- All clients and servers use the same values
Newer protocols allow for an exchange of values (e.g. a Group Exchange protocol)
Example fixed value in older versions of SSH (diffie-hellman-group1-sha1 using Oakley Group 2) $p = 2^{1024} - 2^{960} - 1 + 2^{64} \times (2^{894} \times π + 129093)$

$g = 2$
$p$ is 1024 bits in length

As $p$ and $q$ are public and known to the attacker, using the same values all the time should not be a problem. Exchanging values involves extra communication overhead and also processing overhead. However following the principle of changing keys frequently to give an attacker less chance to compromise them, many protocols now support the ability to change the public parameters.

14.5 Diffie–Hellman in OpenSSL

OpenSSL supports the generation of public parameters for DHKE, as well as of the public and private keys of the users. The calculation of the secret key is also supported, although the public keys need to be manually exchanged. The main operations with OpenSSL are:

Generate global public parameters with genpkey
View parameters with pkeyparam
Generate a public/private key pair with genpkey
Extract a public key with pkey
Derive a shared secret with pkeyutl

For this demo, we use the scenario of user Alice on node1 and Bob on node2. Take note of the prompt to see who is performing each command.

The first step is to generate the Diffie-Hellman (DH) global public parameters, saving them in the file dhp.pem. We use the OpenSSL genpkey command, using the algorithm DH and the -genparam option:

alice@node1:~$ openssl genpkey -genparam -algorithm DH -out dhparam.pem
...+.......................................................................
.............................................................+.............
...............................................+...........................
...........................+........+......................................
.....................................+.....................................
...........................+..................................+........+...
...............+..........+...............+................................
........................................................................+..
..................................................................+........
..............................................+........................+...
.....++*++*++*

Now let’s display the generated global public parameters, first in the encoded form, then in the text form:

alice@node1:~$ cat dhparam.pem
-----BEGIN DH PARAMETERS-----
MIGHAoGBAOZVzJ4E8766527Mp3FD71xEUYdmFan4tPcSuPO99H7n9xfAm7WytmRQ
gxNn2dz4X58FKLzVMY+x2rLyPOd8SLa3OB7tE+gKFMymswteN//lPbFeLWtyei78
                                                                                                                                                  
                                                                                                                                                  
7lGJNnjVDpqJFmo1nldMTDyl5Z+ueZJP5vGGs2ouvem/Cf5N5QRTAgEC
-----END DH PARAMETERS-----

alice@node1:~$ openssl pkeyparam -in dhparam.pem -text
-----BEGIN DH PARAMETERS-----
MIGHAoGBAOZVzJ4E8766527Mp3FD71xEUYdmFan4tPcSuPO99H7n9xfAm7WytmRQ
gxNn2dz4X58FKLzVMY+x2rLyPOd8SLa3OB7tE+gKFMymswteN//lPbFeLWtyei78
7lGJNnjVDpqJFmo1nldMTDyl5Z+ueZJP5vGGs2ouvem/Cf5N5QRTAgEC
-----END DH PARAMETERS-----
PKCS#3 DH Parameters: (1024 bit)
     prime:
         00:e6:55:cc:9e:04:f3:be:ba:e7:6e:cc:a7:71:43:
         ef:5c:44:51:87:66:15:a9:f8:b4:f7:12:b8:f3:bd:
         f4:7e:e7:f7:17:c0:9b:b5:b2:b6:64:50:83:13:67:
         d9:dc:f8:5f:9f:05:28:bc:d5:31:8f:b1:da:b2:f2:
         3c:e7:7c:48:b6:b7:38:1e:ed:13:e8:0a:14:cc:a6:
         b3:0b:5e:37:ff:e5:3d:b1:5e:2d:6b:72:7a:2e:fc:
         ee:51:89:36:78:d5:0e:9a:89:16:6a:35:9e:57:4c:
         4c:3c:a5:e5:9f:ae:79:92:4f:e6:f1:86:b3:6a:2e:
         bd:e9:bf:09:fe:4d:e5:04:53
     generator: 2 (0x2)

Each user can use the public parameters to generate their own private and public key, saving them in their respective files. Similar to RSA, the DH private key file also stores the public key information.

alice@node1:~$ openssl genpkey -paramfile dhparam.pem -out dhprivkey-alice.pem

alice@node1:~$ openssl pkey -in dhprivkey-alice.pem -text -noout
PKCS#3 DH Private-Key: (1024 bit)
     private-key:
         48:88:7d:fd:09:0d:17:5e:33:be:ea:29:e7:b3:83:
         34:29:92:89:06:9f:9a:b4:92:b6:78:07:90:5f:aa:
         98:d9:6d:22:d7:92:05:be:f0:3f:14:af:09:3f:17:
         97:b9:04:73:41:32:c3:4a:38:8f:dc:79:e2:04:97:
         bf:a1:46:5f:ec:2a:ac:4f:ab:df:3b:b0:c9:be:86:
         85:d2:0f:7b:fe:03:46:a9:ab:df:7f:a8:98:38:c3:
         fa:9c:a6:ab:db:70:be:a6:67:95:ab:66:99:cc:15:
         4d:b5:94:90:e4:15:9f:14:2f:7b:dd:ff:60:3c:1d:
         3d:6c:4f:ff:81:77:e1:1d
     public-key:
         00:d9:ab:d7:8c:93:df:dd:eb:92:0d:57:d6:51:31:
         26:d8:f1:11:8c:92:37:a4:51:01:40:8d:bf:fe:6c:
         fd:95:b0:11:a0:16:e4:e0:ab:8a:ef:06:01:e8:36:
         a4:52:b8:bb:88:be:7c:a7:1e:4f:22:f9:7a:a6:5f:
                                                                                                                                                  
                                                                                                                                                  
         83:58:ee:69:34:8d:12:27:d6:5d:b6:e5:36:41:d1:
         a6:54:2a:a4:be:4b:4a:dc:75:fa:c8:16:af:79:a8:
         e3:f5:09:7f:83:13:e7:b7:25:df:37:ea:dc:8c:77:
         4e:20:33:df:a9:9c:95:cc:ef:33:3b:f4:02:b0:66:
         19:8c:30:48:1e:2a:83:87:5c
     prime:
         00:e6:55:cc:9e:04:f3:be:ba:e7:6e:cc:a7:71:43:
         ef:5c:44:51:87:66:15:a9:f8:b4:f7:12:b8:f3:bd:
         f4:7e:e7:f7:17:c0:9b:b5:b2:b6:64:50:83:13:67:
         d9:dc:f8:5f:9f:05:28:bc:d5:31:8f:b1:da:b2:f2:
         3c:e7:7c:48:b6:b7:38:1e:ed:13:e8:0a:14:cc:a6:
         b3:0b:5e:37:ff:e5:3d:b1:5e:2d:6b:72:7a:2e:fc:
         ee:51:89:36:78:d5:0e:9a:89:16:6a:35:9e:57:4c:
         4c:3c:a5:e5:9f:ae:79:92:4f:e6:f1:86:b3:6a:2e:
         bd:e9:bf:09:fe:4d:e5:04:53
     generator: 2 (0x2)

The other user uses the same public parameters, dhparam.pem, to generate their private/public key:

bob@node2:~$ openssl genpkey -paramfile dhparam.pem -out dhprivkey-bob.pem

bob@node2:~$ openssl pkey -in dhprivkey-bob.pem -text -noout
PKCS#3 DH Private-Key: (1024 bit)
     private-key:
         5d:70:9b:3e:a7:c9:b1:3b:df:17:d3:76:dd:45:f0:
         38:6d:be:35:f6:79:5d:05:bf:e2:63:b0:ea:25:00:
         61:0a:4c:e2:e4:e7:8e:97:6e:cb:9e:f0:f9:4b:d9:
         1c:2e:d6:b1:71:cb:ec:56:a7:2f:b0:af:ff:67:df:
         37:e0:d8:8c:ab:5d:ef:3d:27:c5:5a:a6:8d:49:30:
         6b:4e:d4:1f:5c:40:da:35:d0:bc:c7:3d:16:a3:13:
         2e:86:af:13:8b:65:c4:19:f2:75:43:e7:11:b6:5a:
         81:d1:e0:ff:5d:f3:c2:f4:6f:d2:f0:72:97:66:b9:
         93:3d:17:b0:06:ef:8a:3b
     public-key:
         00:d9:9a:00:1b:98:f5:0b:e2:d6:57:f7:4d:e3:4b:
         aa:43:ad:e2:f2:93:31:a1:e7:4b:a7:06:dc:ab:22:
         09:5a:0d:41:1a:c1:37:c0:6d:88:f4:7c:0a:22:27:
         1e:d3:84:39:51:92:62:d5:14:9e:68:ee:2f:69:27:
         ae:dd:d1:e6:a2:5f:3c:d2:7b:a7:7c:8e:61:28:fb:
         8b:1c:d7:a0:0b:d3:7b:37:af:78:b2:7e:eb:62:a7:
         85:b6:0f:90:10:b7:9c:ce:ec:84:a9:28:e3:7f:22:
         8f:76:cd:68:58:56:45:fd:3e:36:37:a1:99:aa:ca:
         4a:65:65:af:a8:21:ee:1f:b6
     prime:
         00:e6:55:cc:9e:04:f3:be:ba:e7:6e:cc:a7:71:43:
         ef:5c:44:51:87:66:15:a9:f8:b4:f7:12:b8:f3:bd:
                                                                                                                                                  
                                                                                                                                                  
         f4:7e:e7:f7:17:c0:9b:b5:b2:b6:64:50:83:13:67:
         d9:dc:f8:5f:9f:05:28:bc:d5:31:8f:b1:da:b2:f2:
         3c:e7:7c:48:b6:b7:38:1e:ed:13:e8:0a:14:cc:a6:
         b3:0b:5e:37:ff:e5:3d:b1:5e:2d:6b:72:7a:2e:fc:
         ee:51:89:36:78:d5:0e:9a:89:16:6a:35:9e:57:4c:
         4c:3c:a5:e5:9f:ae:79:92:4f:e6:f1:86:b3:6a:2e:
         bd:e9:bf:09:fe:4d:e5:04:53
     generator: 2 (0x2)

The users must exchange their public keys. To do so, they must first extract their public keys into separate files using the pkey command

alice@node1:~$ openssl pkey -in dhprivkey-alice.pem -pubout -out dhpub-alice.pem

Bob would perform a similar command as above with his keys (not shown).

We can view the public keys:

alice@node1:~$ openssl pkey -pubin -in dhpub-alice.pem -text
-----BEGIN PUBLIC KEY-----
MIIBIDCBlQYJKoZIhvcNAQMBMIGHAoGBAOZVzJ4E8766527Mp3FD71xEUYdmFan4
tPcSuPO99H7n9xfAm7WytmRQgxNn2dz4X58FKLzVMY+x2rLyPOd8SLa3OB7tE+gK
FMymswteN//lPbFeLWtyei787lGJNnjVDpqJFmo1nldMTDyl5Z+ueZJP5vGGs2ou
vem/Cf5N5QRTAgECA4GFAAKBgQDZq9eMk9/d65INV9ZRMSbY8RGMkjekUQFAjb/+
bP2VsBGgFuTgq4rvBgHoNqRSuLuIvnynHk8i+XqmX4NY7mk0jRIn1l225TZB0aZU
KqS+S0rcdfrIFq95qOP1CX+DE+e3Jd836tyMd04gM9+pnJXM7zM79AKwZhmMMEge
KoOHXA==
-----END PUBLIC KEY-----
PKCS#3 DH Public-Key: (1024 bit)
     public-key:
         00:d9:ab:d7:8c:93:df:dd:eb:92:0d:57:d6:51:31:
         26:d8:f1:11:8c:92:37:a4:51:01:40:8d:bf:fe:6c:
         fd:95:b0:11:a0:16:e4:e0:ab:8a:ef:06:01:e8:36:
         a4:52:b8:bb:88:be:7c:a7:1e:4f:22:f9:7a:a6:5f:
         83:58:ee:69:34:8d:12:27:d6:5d:b6:e5:36:41:d1:
         a6:54:2a:a4:be:4b:4a:dc:75:fa:c8:16:af:79:a8:
         e3:f5:09:7f:83:13:e7:b7:25:df:37:ea:dc:8c:77:
         4e:20:33:df:a9:9c:95:cc:ef:33:3b:f4:02:b0:66:
         19:8c:30:48:1e:2a:83:87:5c
     prime:
         00:e6:55:cc:9e:04:f3:be:ba:e7:6e:cc:a7:71:43:
         ef:5c:44:51:87:66:15:a9:f8:b4:f7:12:b8:f3:bd:
         f4:7e:e7:f7:17:c0:9b:b5:b2:b6:64:50:83:13:67:
         d9:dc:f8:5f:9f:05:28:bc:d5:31:8f:b1:da:b2:f2:
         3c:e7:7c:48:b6:b7:38:1e:ed:13:e8:0a:14:cc:a6:
         b3:0b:5e:37:ff:e5:3d:b1:5e:2d:6b:72:7a:2e:fc:
         ee:51:89:36:78:d5:0e:9a:89:16:6a:35:9e:57:4c:
         4c:3c:a5:e5:9f:ae:79:92:4f:e6:f1:86:b3:6a:2e:
         bd:e9:bf:09:fe:4d:e5:04:53
                                                                                                                                                  
                                                                                                                                                  
     generator: 2 (0x2)

After exchanging public keys, i.e. the files dhpub-alice.pem and dhpub-bob.pem, each user can derive the shared secret. Alice uses her private key and Bob’s public key to derive a secret, in this case a 128 Byte binary value written into the file secret-alice.bin:

alice@node1:~$ openssl pkeyutl -derive -inkey dhprivkey-alice.pem -peerkey dhpubkey-bob.pem -out secret-alice.bin

Bob does the same using his private key and Alice’s public key to produce his secret in the file secret-bob.bin:

bob@node2:~$ openssl pkeyutl -derive -inkey dhprivkey-bob.pem -peerkey dhpub-alice.pem -out secret-bob.bin

The secrets should be the same. Although there is no need for Bob to send his secret file to Alice, if he did, then Alice can use cmp to compare the files, or even xxd to manually inspect the binary values:

alice@node1:~$ cmp secret-alice.bin secret-bob.bin
alice@node1:~$ xxd secret-alice.bin
0000000: b7cb b892 b541 7810 d8ec d089 6c89 3c19  .....Ax.....l.<.
0000010: e8e1 27d8 66ee dac8 684a f0bd 0a7f e7d3  ..'.f...hJ......
0000020: 3643 8654 fddf 4399 e58e 2c7c 3d33 9532  6C.T..C...,|=3.2
0000030: f693 edf2 c9a0 40e8 58b8 38de 74a5 c0b0  ......@.X.8.t...
0000040: 64ab 4006 a3cd d795 2cef d0fc 2b0f d1ab  d.@.....,...+...
0000050: d1e5 1a2a 3431 e3fa ba63 f7cf 1c61 ff65  ...*41...c...a.e
0000060: d9cd c85d c5fe 5c50 c543 aaeb de49 8501  ...]..\P.C...I..
0000070: 6cf1 66a6 87b6 ddec 835c b4b1 3d9d e2fe  l.f......\..=...
alice@node1:~$ xxd secret-bob.bin
0000000: b7cb b892 b541 7810 d8ec d089 6c89 3c19  .....Ax.....l.<.
0000010: e8e1 27d8 66ee dac8 684a f0bd 0a7f e7d3  ..'.f...hJ......
0000020: 3643 8654 fddf 4399 e58e 2c7c 3d33 9532  6C.T..C...,|=3.2
0000030: f693 edf2 c9a0 40e8 58b8 38de 74a5 c0b0  ......@.X.8.t...
0000040: 64ab 4006 a3cd d795 2cef d0fc 2b0f d1ab  d.@.....,...+...
0000050: d1e5 1a2a 3431 e3fa ba63 f7cf 1c61 ff65  ...*41...c...a.e
0000060: d9cd c85d c5fe 5c50 c543 aaeb de49 8501  ...]..\P.C...I..
0000070: 6cf1 66a6 87b6 ddec 835c b4b1 3d9d e2fe  l.f......\..=...

Now both Alice and Bob have a shared secret, securely exchanged across a public network using DHKE.

14.6 DHKE in Python

The Python Cryptography library includes asymmetric algorithms, including RSA. See the examples for DHKE at:

https://cryptography.io/en/latest/hazmat/primitives/asymmetric/

[next] [prev] [prev-tail] [front] [up]

Chapter 14Diffie–Hellman Key Exchange