Chapter 12
Public Key Cryptography
File: crypto/public.tex, r1944
This chapter summarises key concepts in public key cryptography. These concepts will be demonstrated when looking at specific algorithms, including RSA (Chapter 13), Diffie-Hellman Key Exchange (Chapter 14) and Elliptic Curve Cryptography (Chapter 15).
Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).
12.1 Concepts of Public Key Cryptography
We have seen how symmetric key cryptography can be used for encryption. Now let’s look at an alternative approach, public key cryptography.
- Symmetric Key Encryption
- Same key used for encryption and decryption
- Key is randomly generated (e.g. by sender)
- Problem: How does receiver securely obtain secret key?
- Public (or asymmetric) key encryption
- Two different, but mathematically related keys
- One key (public) for encryption, another key (private) for decryption
- Since encrypt key is public, key exchange is not a problem
- Ciphers designed around math problems
- Problem: Performance: much, much slower than symmetric
With symmetric key encryption, assume the sender generates a random key. The receiver of the encrypted data must also know that key in order to decrypt the data. But how does the receiver learn the key? If the sender sends the key unencrypted then an attacker can learn the key and it is no longer secret. If the sender encrypts the key, then the same problem arises: how do they get the second key (which is used to encrypt the first key) to the receiver?
Public key encryption can solve this problem, as we will see in the following slides.
Symmetric key encryption has been the main form of cryptography for a long time. It wasn’t until the 1960’s and 1970’s that public key cryptography was designed.
- Every user has their own key pair: (PU, PR)
- Keys are generated using known algorithm (they are not chosen randomly like symmetric keys)
- Public key, PU
- Available to everyone, e.g. in email signature, on website, in newspaper
- Private key, PR
- Secret, known only by owner, e.g. access restricted file on computer
- Ciphers: if encrypt with one key in the pair, can only successfully decrypt with the other key in the pair
Consider all the students in the class. With public key crypto, each student would generate their own key pair. They could tell everyone their public key (e.g. yell it out in class, print on the screen and show), but they must keep their private key secret. Note that the keys are related: an algorithm is used to generate them (they are not randomly chosen like symmetric key encryption secret keys). That algorithm must be designed such that it is practically impossible for someone to find the private key if they know the public key.
The encryption/decryption algorithms in public key crypto are designed such that if you encrypt plaintext with one key in the pair, then you can only successfully decrypt the ciphertext if using the other key from that pair. For example, if you encrypt a message with the public key of Steve, then you can only decrypt the ciphertext if you know the private key of Steve.
Some public key ciphers also work in the other direction: if you encrypt a message with the private key of Steve, then you can only decrypt the ciphertext if you know the public key of Steve. We will see this in digital signatures.
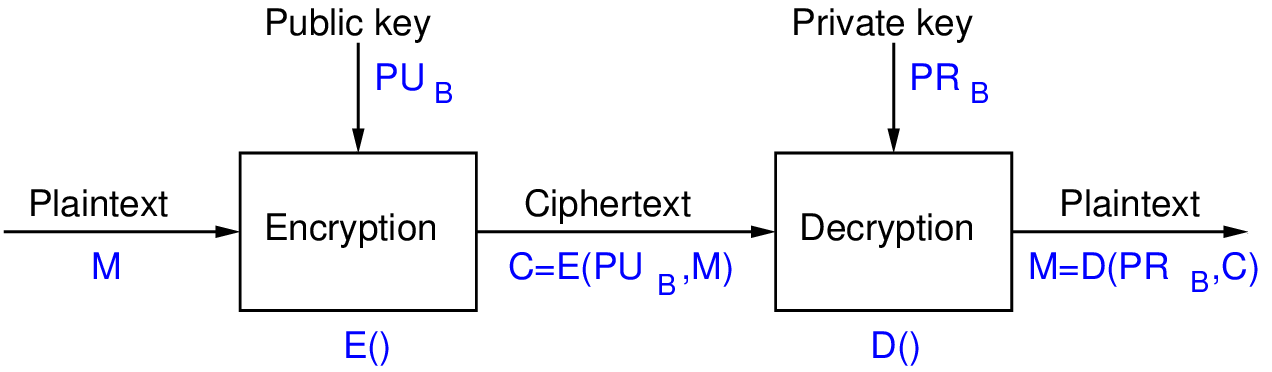
- User A is sender, user B is receiver
- Encrypt using receivers public key,
- Decrypt using receivers private key,
- Only B has , therefore only B can successfully decrypt confidentiality
This assumes User A (on the left ) already knows the public key of user B. Since it is PUBLIC there is no problem with A knowing B’s public key. However in practice, there are problems with A being sure that the public key does indeed belong to B (maybe it is someone pretending to be B). We don’t cover that here, but in the chapter on digital certificates we will see this issue (of knowing who’s public key it is) be addressed.
- Public key ciphers consist of:
- Key generation algorithm
- Encryption algorithm
- Decryption algorithm
- Designed around computationally hard mathematical problems
- Very hard to solve without key, i.e. trapdoor functions
- Finding prime factors of large integers
- Solving logarithms in modulo arithmetic
- Solving logarithms on elliptic curves
The details of the algorithms are covered in subsequent chapters.
- RSA (Rivest Shamir Adleman)
- Security depends on difficult to factor large integers
- Widely used for digital signatures
- Diffie-Hellman
- Security depends on difficult to solve logarithms in modulo arithmetic
- Widely used for secret key exchange
- Elliptic Curve
- Security depends on difficulty to solve logarithms on elliptic curve
- Newer, used in signatures and key exchange
- Smaller keys is benefit
Video: Concepts of Public Key Cryptography (21 min; Apr 2021)