Definition 5.1 (Divides). $b$ divides $a$ if $a=mb$ for some $m$, where $a$, $b$ and $m$ are integers. We can also say $b$ is a divisor of $a$, or $b|a$.

Example 5.1 (Divides). 3 divides 12, since $12=4\times 3$. Also, 3 is a divisor of 12, or $3|12$.

Definition 5.2 (Greatest Common Divisor). $\gcd <!--FUNCTION\; APPLICATION-->\left(a,b\right)$ returns the greatest common divisor of integers $a$ and $b$. There are efficient algorithms for finding the gcd, i.e. Euclidean algorithm.

Example 5.2 (Greatest Common Divisor). $\gcd <!--FUNCTION\; APPLICATION-->\left(12,20\right)=4$, since the divisors of 12 are (1, 2, 3, 4, 6, 12) and the divisors of 20 are (1, 2, 4, 5, 10, 20).

Definition 5.3 (Relatively Prime). Two integers, $a$ and $b$, are relatively prime if $\gcd <!--FUNCTION\; APPLICATION-->\left(a,b\right)=1$.

Example 5.3 (Relatively Prime). $\gcd <!--FUNCTION\; APPLICATION-->\left(7,12\right)=1$, since the divisors of 7 are (1, 7) and the divisors of 12 are (1, 2, 3, 4, 6, 12). Therefore 7 and 12 are relatively prime to each other.

Exercise 5.1 (Relatively Prime). How many positive integers less than 10 are relatively prime with 10?

Solution 5.1 (Relatively Prime). There are 9 positive integers less than 10, i.e. $1,2,3,\dots <!--FUNCTION\; APPLICATION-->,9$. For an integer $a$ to be relatively prime to 10, then $\gcd <!--FUNCTION\; APPLICATION-->\left(a,10\right)=1$. The divisors of 10 are 1, 2, 5 and 10. As the even integers have a divisor of 2, then they cannot be relatively prime with 10. That leaves 1, 3, 5, 7 and 9. $\gcd <!--FUNCTION\; APPLICATION-->\left(5,10\right)=5$ and therefore 5 is not relatively prime with 10. The integers 1, 3, 7 and 9 cannot be divided by 3, 5 or 10, and therefore all have a greatest common divisor with 10 of 1. Hence 1, 3, 7 and 9 are less than 10 and relatively prime with 10. The answer is 4.

Definition 5.4 (Prime Number). An integer $p>1$ is a prime number if and only if its only divisors are $+1$, $-1$, $+p$ and $-p$.

Example 5.4 (Prime Number). The divisors of 13 are (1, 13), that is, 1 and itself. Therefore 13 is a prime number. The divisors of 15 are (1, 3, 5, 15). Since the divisors include numbers other than 1 and itself, 15 is not prime.

Definition 5.5 (Prime Factors). Any integer $a>1$ can be factored as:

where $p_1<p_2<\dots <!--FUNCTION\; APPLICATION--><p_t$ are prime numbers and where each $a_i$ is a positive integer

Example 5.5 (Prime Factors). The following are examples of integers expressed as prime factors:

Exercise 5.2 (Integers as Prime Factors). Find the prime factors of 12870, 12936 and 30607.

Solution 5.2 (Integers as Prime Factors). A naive approach (which works for these small examples) is to check if the number is divisible by primes, in increasing order. For example, is 12870 divisible by 2? Yes, then 2 is a prime factor. Is the result, 6435 divisible by 2? No, then is 6435 divisible by 3? Yes, and so on.

A “cheat” is to use software to find the factors. In Linux command line there is a command called factor.

The answers are:

Definition 5.6 (Prime Factorization Problem). There are no known efficient, non-quantum algorithms that can find the prime factors of a sufficiently large number.

Example 5.6 (Prime Factorization Problem). RSA Challenge involved researchers attempting to factor large numbers. Largest number measured in number of bits or decimal digits. Some records held over time are:

1991: 330 bits or 100 digits

2005: 640 bits or 193 digits

2009: 768 bits or 232 digits

Equivalent of 2000 years on single core 2.2 GHz computer to factor 768 bit

Current algorithms such as RSA rely on numbers of 1024, 2048 and even 4096 bits in length

Definition 5.7 (Euler’s Totient Function). Euler’s totient function, $\varphi \left(n\right)$, is the number of positive integers less than $n$ and relatively prime to $n$. Also written as $\phi \left(n\right)$ or $\text{Tot}\left(n\right)$.

Definition 5.8 (Properties of Euler’s Totient). Several useful properties of Euler’s totient are:

Example 5.7 (Euler’s Totient Function). The integers relatively prime to 10, and less than 10, are: 1, 3, 7, 9. There are 4 such numbers. Therefore $\varphi \left(10\right)=4$.

The integers relatively prime to 11, and less than 11, are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. There are 10 such numbers. Therefore $\varphi \left(11\right)=10$. The property could also be used since 11 is prime.

Since 7 is prime, $\varphi \left(7\right)=6$.

Since $77=7\times 11$, then $\varphi \left(77\right)=\varphi \left(7\times 11\right)=6\times 10=60$.

Definition 5.9 (Modular arithmetic simple). Modular arithmetic is similar to normal arithmetic (addition, subtraction, multiplication, division) but the answers “wrap around”.

Definition 5.10 (mod operator). If $a$ is an integer and $n$ is a positive integer, then $amodn$ is defined as the remainder when $a$ is divided by $n$. $n$ is called the modulus.

Example 5.8 (mod operator). The following are several examples of $mod$:

Definition 5.11 (Congruent modulo). Two integers $a$ and $b$ are congruent modulo $n$ if $\left(amodn\right)=\left(bmodn\right)$. The congruence relation is written as:

$a\equiv b\left(modn\right)$

When the modulus is known from the context, it may be written simply as a $\equiv b$.

Example 5.9 (Congruent modulo). The following are examples of congruence:

Definition 5.12 (Modular arithmetic). Modular arithmetic with modulus $n$ performs arithmetic operations within the confines of set $Z_n=\left\{0,1,2,\dots <!--FUNCTION\; APPLICATION-->,\left(n-1\right)\right\}$.

Example 5.10 (mod in $Z_7$). Consider the set:

All modular arithmetic operations in mod 7 return answers in $Z_7$.

Definition 5.13 (Modular Addition). Addition in mod $n$ is performed as normal addition, with the answer then mod by $n$.

Example 5.11 (Modular Addition). The following are several examples of modular addition:

Definition 5.14 (Additive Inverse). $a$ is the additive inverse of $b$ in mod $n$, if $a+b\equiv 0\left(modn\right)$.

For brevity, AI($a$) may be used to indicate the additive inverse of $a$. One property is that all integers have an additive inverse.

Example 5.12 (Additive Inverse). In mod 7:

In mod 12:

Definition 5.15 (Modular Subtraction). Subtraction in mod $n$ is performed by addition of the additive inverse of the subtracted operand. This is effectively the same as normal subtraction, with the answer then mod by $n$.

Example 5.13 (Modular Subtraction). For brevity, the modulus is sometimes omitted and $=$ is used in replace of $\equiv$. In mod 7:

While the first two examples obviously give answers as we expect from normal subtraction, the third does as well. $1-3=-2$, and in mod 7, $-2\equiv 5$ since $-1\times 7+5=\left(-2\right)$. Recall $Z_7=\left\{0,1,2,3,4,5,6\right\}$.

Definition 5.16 (Modular Multiplication). Modular multiplication is performed as normal multiplication, with the answer then mod by $n$.

Example 5.14 (Modular Multiplication). In mod 7:

Definition 5.17 (Multiplicative Inverse). $a$ is a multiplicative inverse of $b$ in mod $n$ if $a\times b\equiv 1\left(modn\right)$. For brevity, MI($a$) may be used to indicate the multiplicative inverse of $a$. $a$ has a multiplicative inverse in (mod $n$) if $a$ is relatively prime to $n$.

Example 5.15 (Multiplicative Inverse in mod 7). 2 and 7 are relatively prime, therefore 2 has a multiplicative inverse in mod 7.

3 and 7 are relatively prime, therefore 3 has a multiplicative inverse in mod 7.

$\varphi \left(7\right)=6$, meaning 1, 2, 3, 4, 5 and 6 are relatively prime with 7, and therefore all of those numbers have a MI in mod 7.

Example 5.16 (Multiplicative Inverse in mod 8). 3 and 8 are relatively prime, therefore 3 has a multiplicative inverse in mod 8.

4 and 8 are NOT relatively prime, therefore 4 does not have a multiplicative inverse in mod 8. $\varphi \left(8\right)=4$, and therefore only 4 numbers (1, 3, 5, 7) have a MI in mod 8.

Definition 5.18 (Modular Division). Division in mod $n$ is performed as modular multiplication of the multiplicative inverse of 2nd operand. Modular division is only possible when the 2nd operand has a multiplicative inverse, otherwise the operation is undefined.

Example 5.17 (Modular Division). In mod 7:

In mod 8:

$7÷4$ is undefined, since 4 does not have a multiplicative inverse in mod 8.

Definition 5.19 (Properties of Modular Arithmetic).

Commutative, associative and distributive laws similar to normal arithmetic also hold.

Definition 5.20 (Fermat’s Theorem 1). If $p$ is prime and $a$ is a positive integer not divisible by $p$, then:

Definition 5.21 (Fermat’s Theorem 2). If $p$ is prime and $a$ is a positive integer, then:

Example 5.18 (Fermat’s theorem). What is $27^{42}$ mod 43? Since 43 is prime and $42=43-1$, this matches Fermat’s Theorem form 1. Therefore the answer is 1.

Example 5.19 (Fermat’s theorem). What is $640^{163}mod163$? Since 163 is prime, this matches Fermat’s Theorem form 2. Therefore the answer is 640, or simplified to $640mod163=151$.

Definition 5.22 (Euler’s Theorem 1). For every $a$ and $n$ that are relatively prime:

Definition 5.23 (Euler’s Theorem 2). For positive integers $a$ and $n$:

Example 5.20 (Euler’s theorem). Show that $37^{40}mod41=1$. Since $n$ = 41, which is prime, then $\varphi \left(41\right)=40$. As 37 is also prime, 37 and 41 are relatively prime. Therefore Euler’s Theorem form 1 holds.

Example 5.21 (Euler’s theorem). What is $13794^{4621}mod4757$? Factoring 4757 into primes gives $67\times 71$. Therefore $\varphi \left(4757\right)=\varphi \left(67\right)x\times \varphi \left(71\right)=66\times 70=4620$. Therefore, this follows Euler’s Theorem form 2, giving an answer of 13794.

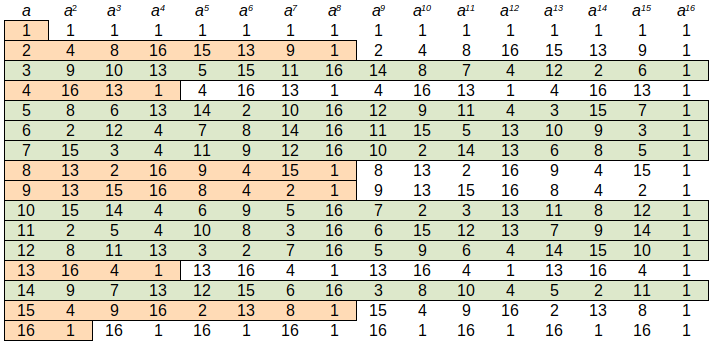
Definition 5.24 (Modular Exponentiation). As exponentiation is just repeated multiplication, modular exponentiation is performed as normal exponentiation with the answer mod by $n$.

Example 5.22 (Modular Exponentiation).

Definition 5.25 (Normal Logarithm). If $b=a^i$, then:

read as “the log in base $a$ of $b$ is index (or exponent) i”.

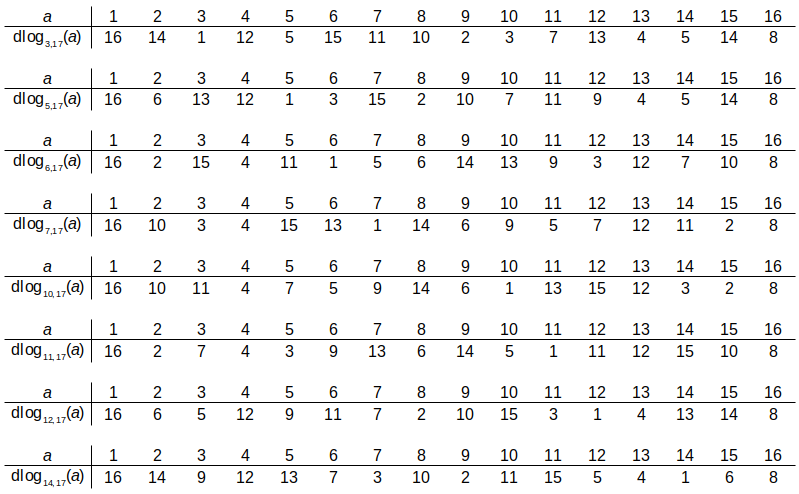
Definition 5.26 (Discrete Logarithm). If $b=a^i\left(modp\right)$, then:

A unique exponent $i$ can be found if $a$ is a primitive root of the prime $p$.

Definition 5.27 (Primitive Root). If $a$ is a primitive root of prime $p$ then $a_1,a_2,a_3,\dots <!--FUNCTION\; APPLICATION-->a_{p-1}$ are distinct in mod $p$.

The integers with a primitive root are: 2, 4, $p^{\alpha }$, $2p^{\alpha }$ where $p$ is any odd prime and $\alpha$ is a positive integer.

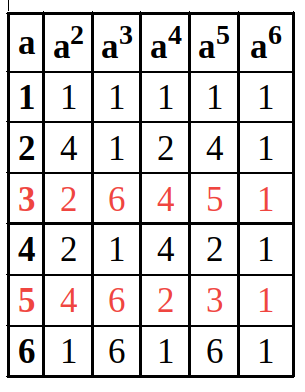
Example 5.23 (Primitive Root). Consider the prime $p=7$:

$a=1:1^{2}mod7=1,1^{3}mod7=1,...\text{(not distinct)}$

$a=2:2^{2}mod7=4,2^{3}mod7=1,2^{4}mod7=2,2^{5}mod7=4,...\text{(not distinct)}$

$a=3:3^{2}mod7=2,3^{3}mod7=6,3^{4}mod7=4,3^{5}mod7=5,3^{6}mod7=1\text{(distinct)}$

Therefore 3 is a primitive root of 7 (but 1 and 2 are not).

Definition 5.28 (Hard Problem: Integer Factorisation). If $p$ and $q$ are unknown primes, given $n=pq$, find $p$ and $q$.

Definition 5.29 (Hard Problem: Euler’s Totient). Given composite $n$, find $\varphi \left(n\right)$.

Definition 5.30 (Hard Problem: Discrete Logarithms). Given $b$, $a$, and $p$, find $i$ such that $i={\text{dlog}}_{a,p}\left(b\right)$.