17 Authentication and Data Integrity

Chapter 17
Authentication and Data Integrity

17.1 Aims of Authentication
17.2 Authentication with Symmetric Key Encryption
17.3 Authentication with Hash Functions
17.4 Authentication with MACs
17.5 Digital Signatures

File: crypto/auth.tex, r1951

This chapter shows how messages can be authenticated, including ensuring data integrity, using various cryptographic primitives, especially hash functions and MACs from Chapter 16.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

17.1 Aims of Authentication

There are different types of attacks that can occur with information transfer. In turn, different mechanisms are available to prevent/detect such attacks.

Disclosure: encryption
Traffic analysis: encryption
Masquerade: message authentication
Content modification: message authentication
Sequence modification: message authentication
Timing modification: message authentication
Source repudiation: digital signatures
Destination repudiation: digital signatures

We have cover encryption primarily from the perspective of preventing disclosure attacks, i.e. providing confidentiality. Now we will look at preventing/detecting masquerade, modification and repudiation attacks using authentication techniques. Note that we consider digital signatures as a form of authentication.

Receiver wants to verify:
1. Contents of the message have not been modified (data authentication)
2. Source of message is who they claim to be (source authentication)
Different approaches available:
- Symmetric Key Encryption
- Hash Functions
- Message Authentication Codes (MACs)
- Public Key Encryption (i.e. Digital Signatures)

We will cover these different approaches in the following sections.

17.2 Authentication with Symmetric Key Encryption

Figure 17.1: Symmetric Encryption for Authentication

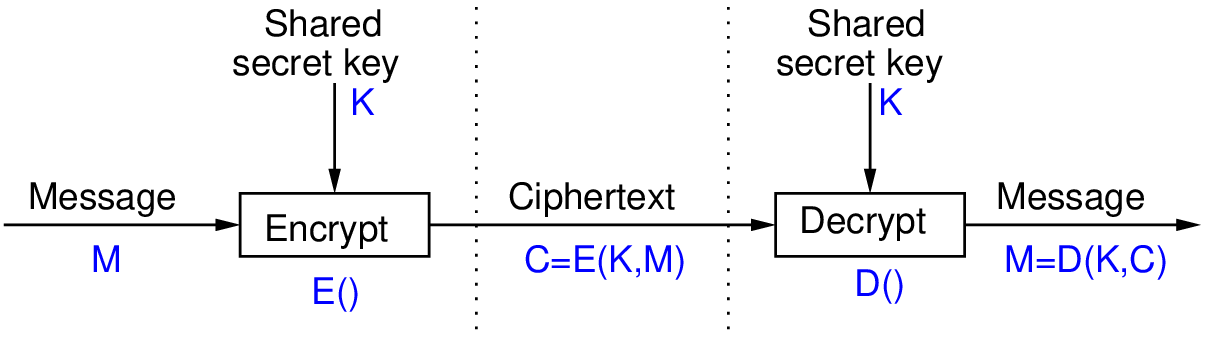
Figure 17.1 shows symmetric key encryption used for confidentiality. On the left is the sender A, and on the right is the receiver B. In the middle (between the dashed lines) is the information sent from A to B. Only B (and A) can recover the plaintext. However in some cases this also provides:

Source Authentication: A is only other user with key; B knows it must have come from A
Data Authentication: successfully decrypted implies data has not been modified

The source and data authentication assumes that the decryptor (B) can recognise that the result of the decryption, i.e. the output plaintext, is correct.

The assumption about being able to recognise the correct plaintext is explored next.

Question 17.1 (Recognising Correct Plaintext in English). $B$ receives ciphertext (supposedly from $A$ , using shared secret key $K$ ):

DPNFCTEJLYONCJAEZRCLASJTDQFY

$B$ decrypts with key $K$ to obtain plaintext:

SECURITYANDCRYPTOGRAPHYISFUN

Was the plaintext encrypted with key $K$ (and hence sent by $A$ )? Is the ciphertext received the same as the ciphertext sent by $A$ ?

The typical answer for above is yes, the plaintext was sent by $A$ and nothing has been modified. This is because the plaintext “makes sense”. Our knowledge of most ciphers (using the English language) is that if the wrong key is used or the ciphertext has been modified, then decrypting will produce an output that does not make sense (not a combination of English words).

Question 17.2 (Recognising Correct Plaintext in English). $B$ receives ciphertext (supposedly from $A$ , using shared secret key $K$ ):

QEFPFPQEBTOLKDJBPPXDBPLOOVX

$B$ decrypts with key $K$ to obtain plaintext:

FTUEUEFTQIDAZSYQEEMSQEADDKM

Was the plaintext encrypted with key $K$ (and hence sent by $A$ )? Is the ciphertext received the same as the ciphertext sent by $A$ ?

Based on the previous argument, the answer is no. Or more precise, either the plaintext was not sent by $A$ , or the ciphertext was modified along the way. This is because the plaintext makes no sense, and we were expected it to do so.

Question 17.3 (Recognising Correct Plaintext in Binary). $B$ receives ciphertext (supposedly from $A$ , using shared secret key $K$ ):

0110100110101101010110111000010

$B$ decrypts with key $K$ to obtain plaintext:

0101110100001101001010100101110

Was the plaintext encrypted with key $K$ (and hence sent by $A$ )? Is the ciphertext received the same as the ciphertext sent by $A$ ?

This is harder. We cannot make a decision without further understanding of the expected structure of the plaintext. What are the plaintext bits supposed to represent? A field in a packet header? A portion of a binary file? A random key? Without further information, the receiver does not know if the plaintext is correct or not. And therefore does not know if the ciphertext was sent by $A$ and has not been modified.

Many forms of information as plaintext can be recognised at correct
However not all, and often not automatically
Authentication should be possible without decryptor having to know context of the information being transferred
Authentication purely via symmetric key encryption is insufficient
Solutions:
- Add structure to information, such as error detecting code
- Use other forms of authentication, e.g. MAC

We will see some of the alternatives in the following sections.

17.3 Authentication with Hash Functions

Figure 17.2: Authentication by Hash and then Encrypt

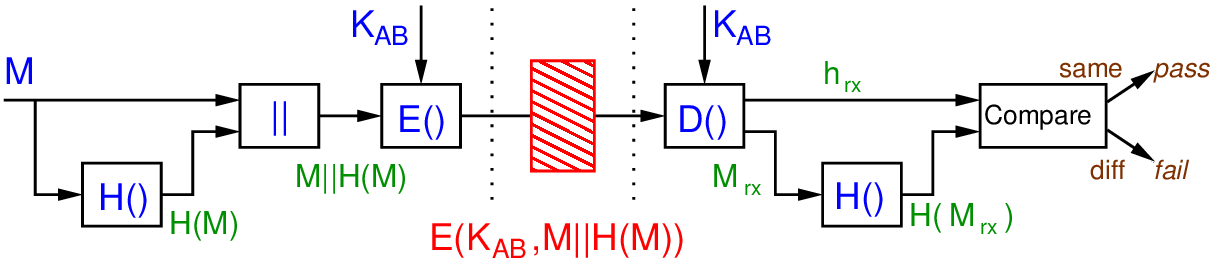
Figure 17.2 shows a scheme where the hash function is used to add structure to the message. Again, user A and B are on the left and right, respectively. The inputs (message and secret key) and operations are shown in blue. The green values are used to refer to intermediate values. In the middle in red is the information sent from A to B.

At the receiver, the “received” message and hash are denoted with a subscript rx. In the normal case (no attack or error), the received values will be identical to the sent values, i.e. $M_{r x} = M$ . However if an attack takes place, then it is possible the sent and received values differ.

When the receiver decrypts, they will be able to determine if the plaintext is correct by comparing the hash of the message component with the stored hash value. This is one method of addressing the problem of using just symmetric key encryption on its own for authentication. This scheme provides confidentiality of the message and authentication.

Figure 17.3: Authentication by Encrypting a Hash

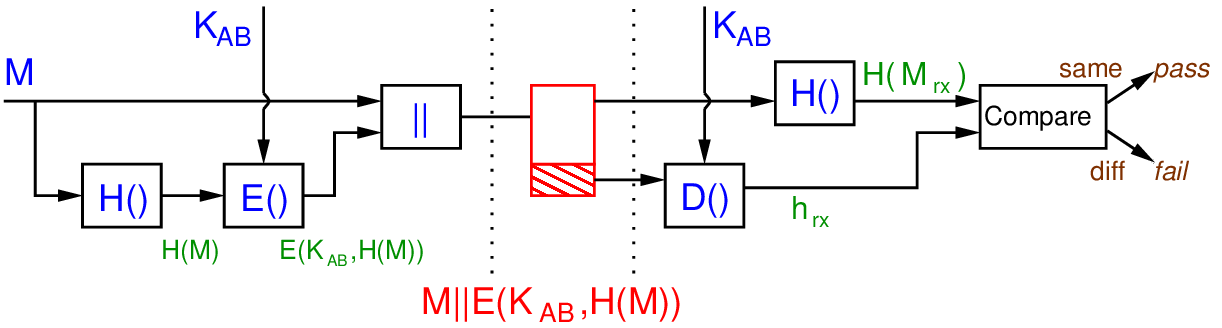
Figure 17.3 shows a different scheme where only the hash value is encrypted. The receiver can verify that nothing has been changed. This scheme provides authentication, but does not attempt to provide confidentiality. This is useful in reducing any computation overhead when confidentiality is not required.

Exercise 17.1 (Attack of Authentication by Encrypting a Hash). If a hash function did not have the Second Preimage Resistant property, then demonstrate an attack on the scheme in Figure 17.3.

Solution 17.1 (Attack of Authentication by Encrypting a Hash). The attacker intercepts the message $M | | E (K, H (M))$ before it reaches B. If the Second Preimage Resistant property does not hold, then it is possible for an attacker to find another message $M^{'}$ where $H (M) = H (M^{'})$ . As a result, the attacker can modify $M$ to $M^{'}$ , but leave the remainder of the sent information, $E (K, H (M))$ as is. They forward $M^{'} | | E (K, H (M))$ to $B$ . User $B$ decrypts with the key shared with $A$ , then compare the hash value with $H (M^{'})$ . They match. Therefore user $B$ trusts the message, but in fact it has been subject to a modification attack.

Figure 17.4: Authentication with Hash of a Shared Secret

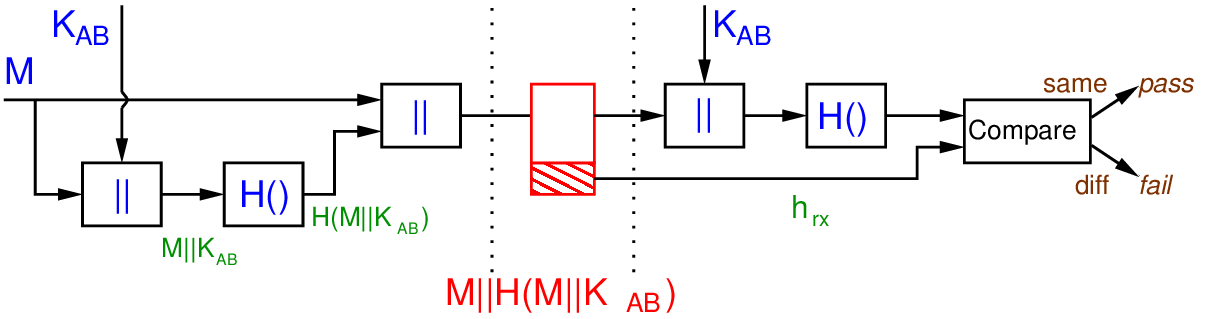
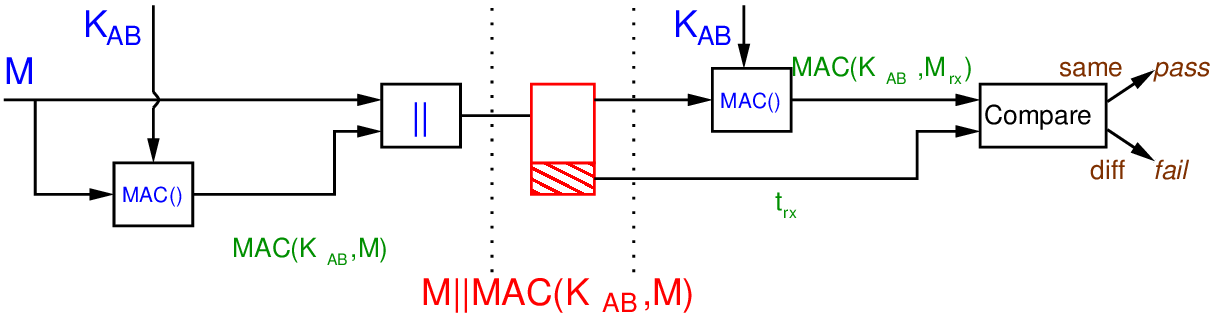
Figure 17.4 shows a scheme the provides authentication, but without using any encryption. Avoiding encryption can be desirable in very resource constrained environments. $S$ is a secret value shared by $A$ and $B$ . Concatenating the secret with the message, and then hashing the result, allows the receiver the verify the plaintext is correct, and keeps the secret confidential.

Exercise 17.2 (Attack of Authentication with Hash of Shared Secret). If a hash function did not have the Preimage Resistant property, then demonstrate an attack on the scheme in Figure 17.4.

Solution 17.2 (Attack of Authentication with Hash of Shared Secret). The attacker intercepts the message $M | | H (M | | S)$ . If the Preimage Resistant property does not hold, then it is possible for an attacker, given a hash value, to find the original input, i.e. the preimage. That is the attacker find $M | | S$ . Since they also know $M$ , it is easy to find $S$ , i.e. the remaining bits. The attacker now knows the shared secret and could masquerade as $A$ .

In Section 17.5 we will see the role of hash functions in digital signatures.

17.4 Authentication with MACs

MACs can be used for authentication by themselves, or combined with symmetric key encryption (e.g. when confidentiality is also required). First we look at using only MACs.

Figure 17.5: Authentication with only MACs

Figure 17.5 shows a scheme where authentication is provided using only a MAC. That is, encryption is not used.

Now we consider the case of combining MACs with encryption.

Common to what both confidentiality and authentication (data integrity)
MACs have advantage over hashes in that if encryption is defeated, then MAC still provides integrity
But two keys must be managed: encryption key and MAC key
Recommended algorithms used for encryption and MAC are independent
Three general approaches (following definitions), referred to as authenticated encryption

Definition 17.1 (Encrypt-then-MAC). The sender encrypts the message $M$ with symmetric key encryption, then applies a MAC function on the ciphertext. The ciphertext and the tag are sent, as follows:

E (K_{1}, M) | | M A C (K_{2}, E (K_{1}, M))

Two independent keys, $K_{1}$ and $K_{2}$ , are used.

Definition 17.2 (MAC-then-Encrypt). The sender applies a MAC function on the plaintext, appends the result to the plaintext, and then encrypt both. The ciphertext is sent, as follows:

E (K_{1}, M | | M A C (K_{2}, M))

Definition 17.3 (Encrypt-and-MAC). The sender encrypts the plaintext, as well ass applying a MAC function on the plaintext, then combines the two results. The ciphertext joined with tag are sent, as follows:

E (K_{1}, M) | | M A C (K_{2}, M)

Which of the three approaches is better?

There are small but important trade-offs between encrypt-then-MAC, MAC-then-encrypt and encrypt-and-MAC
Potential attacks on each, especially if a mistake in applying them
Generally, encrypt-then-MAC is recommended, but are cases against it
Some discussion of issues:
- Chapter 9.6.5 of Handbook of Cryptography
- Moxie Marlinspike
- StackExchange
- Section 1 and 2 of Authenticated Encryption by J Black
Other authenticated encryption approaches incorporate authenticate into encryption algorithm
- AES-GCM, AES-CCM, ChaCha20 and Poly1305

It is worth reading some of the discussion about the three approaches.

17.5 Digital Signatures

Authentication has two aims:
- Authenticate data: ensure data is not modified
- Authenticate users: ensure data came from correct user
Symmetric key crypto, MAC functions are used for authentication
- But cannot prove which user created the data since two users have the same key
Public key crypto for authentication
- Can prove that data came from only 1 possible user, since only 1 user has the private key
Digital signature
- Encrypt hash of message using private key of signer

A digital signature has the same purpose of a handwritten signature: to prove that a document (or message or file) is approved by and originated from one particular person. If a message is signed, the signer cannot claim they did not sign it (since they are the only person that could create the signature). Similar, someone cannot pretend to be someone else, since they cannot create that other persons signature. Of course handwritten signatures are imprecise and sometimes forgeable. Digital signatures are much more secure, making it practically impossible for someone to forge a signature or modify a signed document without it being noticed.

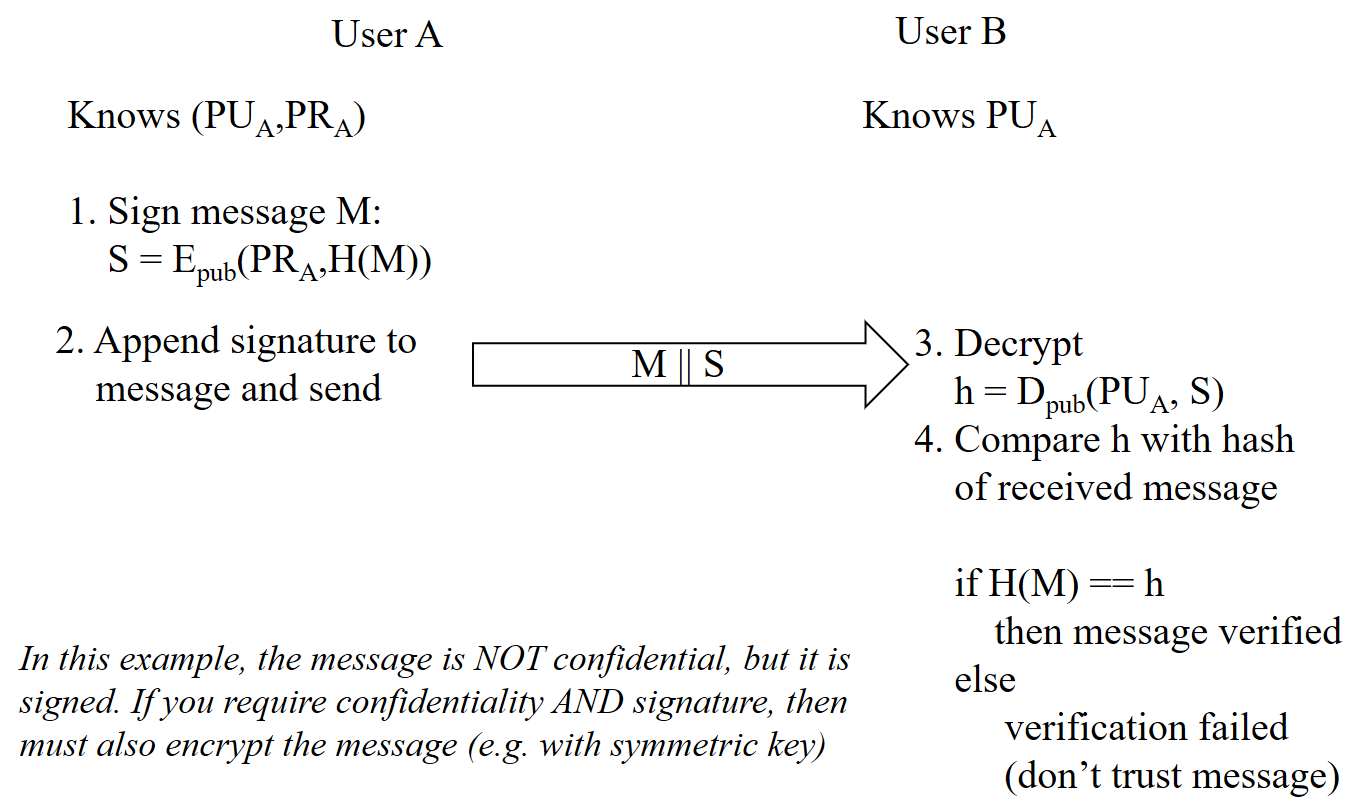
In practice, a digital signature of a message is created by first calculating a hash of that message, and then encrypting that hash value with the private key of the signer. The signature is then attached to the message.

The hash function is not necessary for security, but makes signatures practical (the signature is short fixed size, no matter how long the message is).

User A has own key pair: $(P U_{A}, P R_{A})$
Signing
- User A signs a message by encrypting hash of message with own private key: $S = E (P R_{A}, H (M))$
- User attaches signature S to message M and sends to user B
Verification
- User B verifies a message by decrypting signature with signer’s public key: $h = D (P U_{A}, S)$
- User B then compares hash of received message, $H (M)$ , with decrypted $h$ ; if identical, signature is verified

Figure 17.6: Digital Signature Example

[prev] [prev-tail] [front] [up]

Chapter 17Authentication and Data Integrity

17.1 Aims of Authentication

17.2 Authentication with Symmetric Key Encryption

17.3 Authentication with Hash Functions

17.4 Authentication with MACs

17.5 Digital Signatures

Chapter 17
Authentication and Data Integrity