16 Hash Functions and MACs

Chapter 16
Hash Functions and MACs

16.1 Informal Overview of Hashes and MACs
16.2 Introduction to Hash Functions
16.3 Properties of Cryptographic Hash Functions
16.4 Introduction to Message Authentication Codes

File: crypto/hash.tex, r1951

This chapter introduces two primitives used in authentication and data integrity: cryptographic hash functions and Message Authentication Codes. While these primitives can be based on symmetric key ciphers (and occasionally public key ciphers), in many cases they are custom-designed algorithms to meet the specific needs for authentication.

Presentation slides that accompany this chapter can be downloaded in the following formats: slides only (PDF); slides with notes (PDF, ODP, PPTX).

16.1 Informal Overview of Hashes and MACs

We will start with an informal overview of the concepts, terminology, security goals and applications. We will primarily refer to hash functions and Message Authentication Codes.

Hash functions
- Takes message as input and returns short, unique and random-looking output
- Different inputs will produce different outputs
- Also called: Modification Detection Code (MDC), unkeyed hash function
- Output called: hash ( $h$ ), digital fingerprint, imprint, message digest
- $h = H (M)$
Message Authentication Code (MAC)
- Takes message and a secret key as input and returns short, unique and random-looking output
- Different inputs (key and/or data) will produce different outputs
- Also called: keyed hash function
- Output called: tag ( $t$ ), code or MAC
- $t = M A C (K, M)$

Chapter 9 of the Handbook of Applied Cryptography explains the different classifications of hash functions.

Also note that our focus is on cryptographic purposes of hashes and MACs. They have other, non-crypto applications, e.g. hash functions for caching. To be more precise we should refer to cryptographic hash functions, however for brevity we often just refer to hash functions.

Pre-image resistance (one-way)
- Given the output (hash/tag), attacker cannot find the input message
Second pre-image resistance (weak collision resistance)
- Given one message, attacker cannot find another message with same output (hash/tag)
Collision resistance (strong collision resistance)
- Attacker cannot find any two messages that produce same output (hash/tag)

Note that there is different terminology used for the properties. The names in parentheses are an alternative form.

The first two properties are similar from a security perspective: most algorithms that have one property also have the other. However the third property of (strong) collision resistance is harder to provide. That is, some algorithms may have the first two properties, but not the third of (strong) collision resistance.

Digital signature (public key crypto + hash)
- preimage, 2nd preimage, collision resistance (if attacker can perform chosen message attack)
Message authentication with symmetric key encryption and hash
- none
Message authentication with MAC only
- preimage, 2nd preimage, collision resistance (if attacker can perform chosen message attack)
Message authentication using hash only
- Assumes an authentic channel, where delivery of hash is trusted
- 2nd preimage resistant
Password storage with hash
- preimage resistant

16.2 Introduction to Hash Functions

Hash functions are algorithms used in different aspects of computing and IT, and especially important in cryptography. We often distinguish between different hash functions used for general computing purposes versus those used in cryptography based on the properties of the function.

Hash function or algorithm H():
- Input: variable-length block of data $M$
- Output: fixed-length, small, hash value, $h$ , where $h = H (M)$
- Another name for hash value is digest
- Output hash values should be evenly distributed and appear random
A secure, cryptographic hash function is practically impossible to:
- Find the original input given the hash value
- Find two inputs that produce the same hash value

A hash function is an algorithm that usually takes any sized input, like a file or a message, and produces a short (e.g. 128 bit, 512 bit) random looking output, the hash value. If you apply the hash function on the same input, you will always get the exact same hash value as output. In practice, if you apply the hash function on two different inputs, you will get two different hash values as output.

Message authentication
Digital signatures
Storing passwords
Signatures of data for malicious behaviour detection (e.g. virus, intrusion)
Generating pseudorandom number

Hash functions are important in many areas of security. They are typically used to create a fingerprint/signature/digest of some input data, and then later that fingerprint is used to identify if the data has been changed. However they also have uses for hiding original data (storing passwords) and generating random data. Different applications may have slightly different requirements regarding the security (and performance) properties of hash functions.

There are three general approaches to design hash functions:

Based on Block Ciphers: Well-known and studied block ciphers are used with a mode of operation to produce a hash function. Generally, less efficient than customised hash functions.
Based on Modular Arithmetic: Similar motivation as to basing on block ciphers, but based on public key principles. Output length can be any value. Precautions are needed to prevent attacks that exploit mathematical structure.
Customised Hash Functions: Functions designed for the specific purpose of hashing. Disadvantage is they haven’t been studied as much as block ciphers, so harder to design secure functions.

Designing hash functions based on existing cryptographic primitives is advantageous in that existing knowledge and implementations can be re-used. However as more time has been spent studying customised hash functions, they are now the approach of choice due to their security and efficiency.

While a number of cryptographic hash functions have been designed over the years, the two main ones of interest are MD5 and SHA.

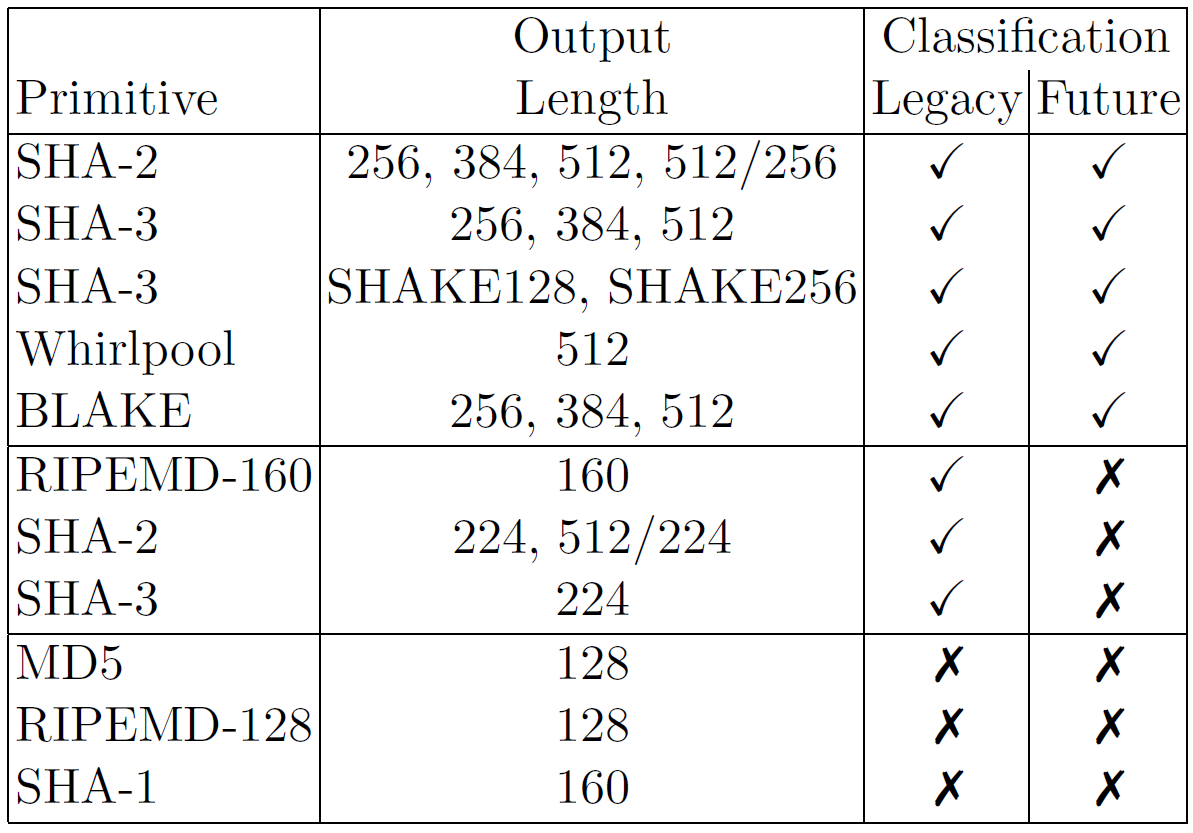
Credit: ECRYPT CSA Algorithms, Key Size and Protocols Report, 2018

Figure 16.1: Selected Cryptographic Hash Functions

Figure 16.1 shows selected hash functions, classified for legacy or future use. It is taken from the ECRYPT-CSA 2018 report on Algorithms, Key Sizes and Protocols. The authors classified hash functions as legacy, meaning secure for near future, and future, meaning secure for medium term. It includes history hash functions no longer recommended, such as MD5, RIPEMD-128 and SHA-1. There are many other hash functions. Wikipedia has a nice comparison.

16.3 Properties of Cryptographic Hash Functions

Definition 16.1 (Pre-image of a Hash Value). For hash value $h = H (x)$ , $x$ is pre-image of $h$ . As $H$ is a many-to-one mapping, $h$ has multiple pre-images. If $H$ takes a $b$ -bit input, and produces a $n$ -bit hash value where $b > n$ , then each hash value has $2^{b - n}$ pre-images.

A hash function takes a single input and produces a single output. The output is the hash value and the input is the pre-image of that hash value.

Definition 16.2 (Hash Collision). A collision occurs if $x \neq y$ and $H (x) = H (y)$ . Collisions are undesirable in cryptographic hash functions.

We will show shortly that collisions should be practically impossible to be found by an attacker.

Exercise 16.1 (Number of Collisions). If $H 1$ takes fixed length 200-bit messages as input, and produces a 80-bit hash value as output, are collisions possible?

Solution 16.1 (Number of Collisions). Yes. In this simplistic example (since hash functions normally take variable length messages), there are $2^{200}$ possible different inputs. A hash function maps an input to an output hash value. There are $2^{80}$ possible output hash values. That means at least two of the inputs must map to the same output hash value, i.e. a collision. Assuming the hash function distributes the pre-images to hash values in a uniformly random manner, then on average, each hash value has $2^{200 - 80} = 2^{120}$ pre-images.

The point is, that if the input message length is larger than the output hash value (and in practice, it always is), then collisions are theoretically possible. One aspect of designing cryptographically secure hash functions is to make it practical impossible for an attacker to find useful collisions.

Now let’s restate the general requirements of a cryptographic hash function.

Variable input size:: $H$ can be applied to input block of any size
Fixed output size:: $H$ produces fixed length output
Efficiency:: $H (x)$ relatively easy to compute (practical implementations)
Pseudo-randomness:: Output of $H$ meets standard tests for pseudo-randomness
Properties:: Satisfies one or more of the properties: Pre-image Resistant, Second Pre-image Resistant, Collision Resistant

Now let’s define several common required properties of cryptographic hash functions.

Definition 16.3 (Pre-image Resistant Property). For any given $h$ , it is computationally infeasible to find $y$ such that $H (y) = h$ . Also called the one-way property.

Informally, it is hard to inverse the hash function. That is, given the output hash value, find the original input message.

Definition 16.4 (Second Pre-image Resistant Property). For any given $x$ , it is computationally infeasible to find $y \neq x$ with $H (y) = H (x)$ . Also called weak collision resistant property.

To break this property, the attacker is trying to find a collision. That is, two input messages $x$ and $y$ that produce the same output hash value. Importantly, the attacker cannot choose $x$ . They are given $x$ and must find a different message $y$ that produces a collision.

Definition 16.5 (Collision Resistant Property). It is computationally infeasible to find any pair $(x, y)$ such that $H (x) = H (y)$ . Also called strong collision resistant property.

To break this property, again the attacker is trying to find a collision. However in this case the attacker has the freedom to find any messages $x$ and $y$ that produce a collision. This freedom makes it easier for the attacker to perform an attack against this property than against the Second Pre-image Resistant property.

Pre-image and Second Pre-image Attack
- Find a $y$ that gives specific $h$ ; try all possible values of $y$
- With $b$ -bit hash code, effort required proportional to $2^{b}$
Collision Resistant Attack
- Find any two messages that have same hash values
- Effort required is proportional to $2^{b ∕ 2}$
- Due to birthday paradox, easier than pre-image attacks

Exercise 16.2 (Brute Force Attack on Hash Function). Consider a hash function to be selected for use for digital signatures. Assume an attacker has compute capabilities to calculate $1 0^{12}$ hashes per second and is prepared to wait for approximately 10 days for a brute attack. Find the minimum hash value length that the hash function should support, such that a brute force is not possible.

Solution 16.2 (Brute Force Attack on Hash Function). There are two cases to consider. If the hash function and network is subject to a chosen message attack, then the hash function should support all three properties. Preimage and Second Preimage Resistant properties required effort of approximately $2^{b}$ for the attacker. But attacking Collision Resistant property requires significantly less effort, $2^{b ∕ 2}$ . Therefore the hash length, $b$ , must be sufficient so that an attack on Collision Resistant property is not possible.

\begin{array}{rcl} \frac{2^{b ∕ 2}}{1 0^{12}} & > & 10 \times 24 \times 60 \times 60 \\ 2^{b ∕ 2} & > & 1 0^{12} \times 10 \times 86400 \\ b ∕ 2 & > & l o g_{2} (8.64 \times 1 0^{17}) \\ b ∕ 2 & > & 59.583 \\ b & > & 119.168 \end{array}

Therefore the hash length, $b$ , should be at least 120 bits.

If however a chosen message attack is not possible, then the hash function only needs to meet the Preimage and Second Preimage Resistant properties. Therefore only a 60 bit hash length is needed (i.e. a weaker hash function).

16.4 Introduction to Message Authentication Codes

In the above we looked at cryptographic hash functions that take a message as input and produce a hash value as output. One application of hash functions is authentication, as we will see in depth in Chapter 17. However note that hash functions do not use any secret key as input. A variation is to introduce a secret key as input, resulting in a keyed hash function.

Hash functions have no secret key
- Can be referred to as unkeyed hash function
- Also called Modification Detection Code
A variation is to allow a secret key as input, in addition to the message
- $h = H (K, M)$
- Keyed hash function or Message Authentication Code (MAC)
Hashes and MACs can be used for message authentication, but hashes also used for multiple other purposes
MACs are more common for authentication messages

Now we will shift our focus to MACs, first looking at the general design approaches.

Based on Block Ciphers: CBC-MAC, OMAC, PMAC,
Customised MACs: MAA, MD5-MAC, UMAC, Poly1305
Based on Hash Functions: HMAC

The motivation for different design approaches is similar to that for hash function design approaches.

Definition 16.6 (Computation Resistance of MAC). Given one or more text-tag pairs, $[x_{i}, MAC (K, x_{i})]$ , computationally infeasible to compute any text-tag pair $[y, MAC (K, y)]$ , for a new input $y \neq x_{i}$

Assume an attacker has intercepted messages (text) and the corresponding MACs (tags). They have $i$ such text-tag pairs. Now there is a new message $y$ . It should be practically impossible for the attacker to find the corresponding tag of $y$ , that is, $MAC (K, y)$ .

Given what the attacker must do, the security of MACs can be defined based on the effort of brute force attacks.

Brute Force Attack on Key
- Attacker knows $[x_{1}, T_{1}]$ where $T_{1} = M A C (K, x_{1})$
- Key size of $k$ bits: brute force on key, $2^{k}$
- But …many tags match $T_{1}$
- For keys that produce tag $T_{1}$ , try again with $[x_{2}, T_{2}]$
- Effort to find $K$ is approximately $2^{k}$
Brute Force Attack on MAC value
- For $x_{m}$ , find $T_{m}$ without knowing $K$
- Similar effort required as one-way/weak collision resistant property for hash functions
- For $n$ bit MAC value length, effort is $2^{n}$
Effort to break MAC: $m i n (2^{k}, 2^{n})$

[next] [front] [up]

Chapter 16Hash Functions and MACs

16.1 Informal Overview of Hashes and MACs

16.2 Introduction to Hash Functions

16.3 Properties of Cryptographic Hash Functions

16.4 Introduction to Message Authentication Codes

Chapter 16
Hash Functions and MACs