Impact of Noise on Sine Wave Compared to Square Wave
My last post showed how to use sox and Audacity to generate and view sinusoid signals. This is useful for quick demonstration of basic concepts of communication signals. The following is one such demo: showing how noise impacts on different shaped signals in different ways. In particular, how a communications signal with few frequency components (e.g. sine wave) has increased chance of bit errors in presence of noise when compared to those with many frequency components (e.g. square wave).
For further details of these concepts see my lecture on data transmission for ITS323 (lecture notes, video). If you don't want to generate the signals using sox you can download them below. They can be opened in Audacity and probably many other audio editors.
Generate a 1000 Hz sine wave with duration 10ms. This is the transmitted sine signal.
$ sox --null sine1000.wav synth 0.01 sine 1000
Noise will be generated such that it is low for most of the 10ms transmission (i.e. from 0 to 5.5ms and from 6ms to 10ms), quite high and positive (60% DC offset) for a short 0.5ms burst (starting at time 5.5ms).
$ sox --null noise1.wav synth 0.0055 whitenoise
$ sox --null noise2.wav synth 0.0005 60 whitenoise
$ sox --null noise3.wav synth 0.004 whitenoise
Concatenate the three noise segments to obtain 10ms of noise:
$ sox --combine concatenate --volume 0.2 noise1.wav --volume 0.6 noise2.wav --volume 0.2 noise3.wav noise.wav
Mix the transmitted sine wave with the noise to obtain the received signal.
$ sox --combine mix --volume 0.3 sine1000.wav --volume 0.7 noise.wav sinenoise.wav
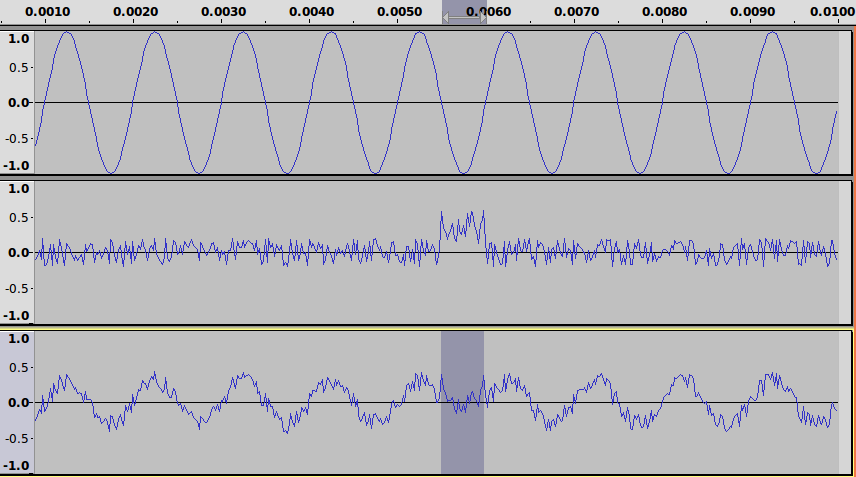
The three signals (transmitted, noise and received) are plotted below in Audacity. The portion highlighted on the received signal has an average value which is positive, when the transmitted signal at the same time was negative. That is, the receiver assumes a high signal received (e.g. bit 1) when in fact a low signal was transmitted (e.g. bit 0). A bit error occurs.
Now lets see how the exact same noise impacts on a transmitted square wave. Generate a 1000Hz square wave:
$ sox --null square1000.wav synth 0.01 square 1000
Mix the square wave with the same noise signal as used above to produce the received signal.
$ sox --combine mix --volume 0.3 square1000.wav --volume 0.7 noise.wav squarenoise.wav
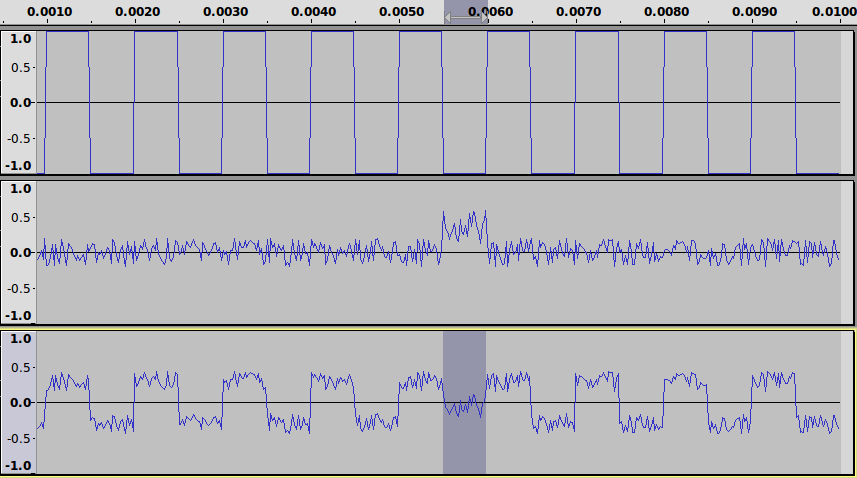
Below are the three signals. The highlighted portion is on average negative. In this case the received bit (low, 0) is the same as transmitted (low, 0). There is no bit error.
Although a very simplistic example, the main point is that the closer the transmitted signal is to a square wave, the less chance bit errors will occur.
Created on Thu, 19 Jul 2012, 7:18pm
Last changed on Fri, 21 Jun 2013, 6:07pm